5.2 固有モードの二次効果
そこで今度は全ての二次効果を考慮に入れる。
変数を次のように基本場(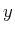 方向に一様)・擾乱成分・擾乱の二次オーダーの帯状成分に分ける。
方向に一様)・擾乱成分・擾乱の二次オーダーの帯状成分に分ける。
擾乱成分は摂動方程式(10),(11)に従い時間発展する。線形安定性解析で求まる発達率を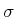 と書くと
と書くと
擾乱の二次オーダーの帯状成分に関する式は、式(2),(7)より次のようになる。
この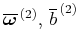 に関する微分方程式を解く。
に関する微分方程式を解く。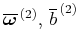 をスペクトル法を用いて
をスペクトル法を用いて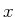 -
-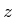 面で離散化し、全スペクトル成分(
面で離散化し、全スペクトル成分(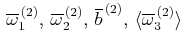 )をまとめてベクトル
)をまとめてベクトル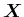 と書くと、(17),(18)は次のようになる。
と書くと、(17),(18)は次のようになる。
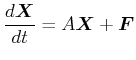 |
(19) |
ここで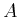 は係数行列、
は係数行列、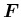 は(17),(18)それぞれの右辺第1項(擾乱同士の相互作用の効果)であり、
は(17),(18)それぞれの右辺第1項(擾乱同士の相互作用の効果)であり、
と書ける(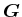 は空間構造を表すベクトル、発達率は擾乱の発達率の2倍になっていることに注意)。まず、(19)の特解を
は空間構造を表すベクトル、発達率は擾乱の発達率の2倍になっていることに注意)。まず、(19)の特解を
として(19)に代入すると、次が得られる。
ここで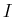 は単位行列である。これを
は単位行列である。これを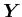 について解けば特解(20)が求まる。(19)の一般解は
について解けば特解(20)が求まる。(19)の一般解は
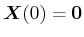 とすると
とすると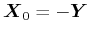 となり、次の一般解が得られる。
となり、次の一般解が得られる。
上式中の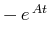 は減衰振動成分であり、時間が経過すると
は減衰振動成分であり、時間が経過すると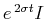 の項が卓越する。よって、特解
の項が卓越する。よって、特解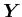 の構造が、固有モードの二次効果による平均流加速の分布を決定する。
の構造が、固有モードの二次効果による平均流加速の分布を決定する。
さて、平均流の加速を表す量は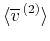 である。ここで、
である。ここで、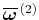 と
と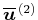 の間には次の関係がある。
の間には次の関係がある。
求めた特解の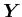 の
の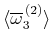 成分から(25)を用いて計算した
成分から(25)を用いて計算した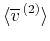 の
の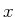 分布を図24に示す。
分布を図24に示す。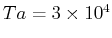 の場合は図21と図24(左)、
の場合は図21と図24(左)、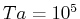 の場合は図22と図24(右)で、いずれも加速の分布が一致している。したがって、平均流の加速は、(17),(18)の右辺第1項以外、すなわち擾乱の二次オーダーの帯状成分に関する項からの寄与が大きいことが分かる。
の場合は図22と図24(右)で、いずれも加速の分布が一致している。したがって、平均流の加速は、(17),(18)の右辺第1項以外、すなわち擾乱の二次オーダーの帯状成分に関する項からの寄与が大きいことが分かる。
図24:
固有モードの二次効果による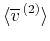 の
の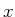 分布。(左:
分布。(左: 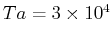 、右:
、右: 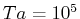 )
)
|
|
SAITO Naoaki
2009-07-09
![]() 方向に一様)・擾乱成分・擾乱の二次オーダーの帯状成分に分ける。
方向に一様)・擾乱成分・擾乱の二次オーダーの帯状成分に分ける。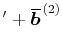
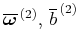 に関する微分方程式を解く。
に関する微分方程式を解く。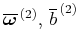 をスペクトル法を用いて
をスペクトル法を用いて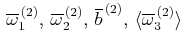 )をまとめてベクトル
)をまとめてベクトル![]() である。ここで、
である。ここで、![]() と
と![]() の間には次の関係がある。
の間には次の関係がある。