付録 A.1 赤道波における wave-CISK

地球の熱帯における大気運動の考察においては, メトリックの緯度変化は無視しコリオリパラメタを緯度に比例させる 「赤道ベータ平面近似」がしばしば用いられる. この枠組みにおいて, 鉛直成層した3次元ブジネスク流体の熱源応答を記述する, 線形化方程式は以下のようになる.

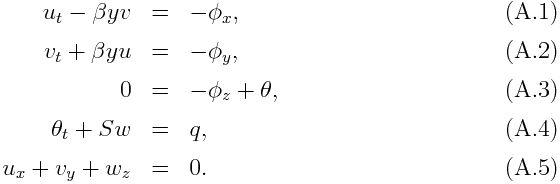
ここで, (x, y, z) はそれぞれ北向き, 東向き, 鉛直上向き座標, ただし y=0 が赤道, (u, v, w) はそれぞれ速度の北向き, 東向き, 鉛直上向き成分, Φ は高度, θは温度偏差, S は基本場の温度勾配, q は凝結加熱である. また, 下付き添え字は、その変数についての偏微分を表す.

Hayashi(1970)の　wave-CISK の定式化では、 凝結加熱 q は

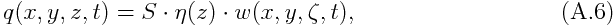
のように, その鉛直構造が, 時間変化・水平分布と分離されると仮定して表現される. ここでζは大気境界層上端の高度であり, 典型的には1km程度が想定される. この定式化では, 雲活動と大規模運動の間に「スケール分離」が成り立つことが仮定されており, 雲活動は q の表現に圧縮され, 上記方程式系が記述するのは大規模運動である. 熱帯大気中の加熱の主役である積乱雲が, 下層の上昇運動をきっかけとして発生し, その後, 大規模運動の時間スケール(数日程度)と比較して極めて短い時間(1時間程度)で 圏界面まで成長して対流圏の全体を加熱することを想定したものである.

この定式化が現実大気中の加熱のモデル化としてどの程度妥当であるか については, 当然, 多くの議論があるが, ここでは立ち入らない. ここで付け加えておくべき重要な注意は Kuo スキーム との関係である. 本論文での数値実験でも用いた Kuo スキーム における 雲活動による加熱の計算では, その総量が下層大気の水蒸気の収束から算出されるが, これは近似的に下層の上昇流に比例する. また, 加熱の鉛直構造は大気の温度構造から決定されるが, 熱帯大気の 温度構造が水平方向の変化に乏しいことを考慮すると, 近似的には固定した構造をもつとして扱える. これらのことから Kuo スキーム における加熱は, 上の単純な定式化に近いものとなる.

これらの式は, 東西方向および時間方向に周期性を仮定し, 全ての変数が

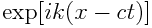
に比例すると置くことにより, 鉛直・南北依存性についても変数分離することができる. ここで東西位相速度 c は複素数であることを許容する. その虚部が正であれば擾乱が指数関数的に成長することを意味する. 実際に

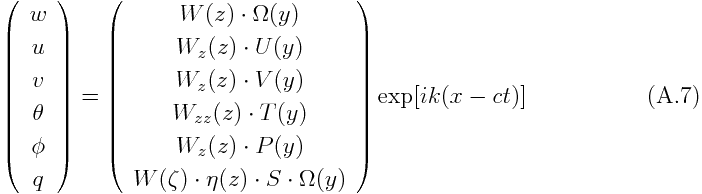
とおいて整理すると, 鉛直構造方程式をW(z)について

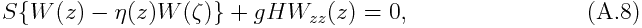
水平構造方程式を U(y),V(y),P(y) について

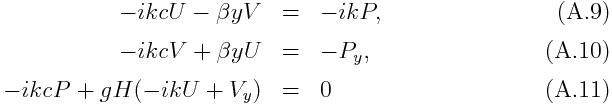
の様に得ることができる. ここで現れる分離定数 H は等価深度と呼ばれる. g は重力加速度であり, 分離定数が長さの次元を持ち, 水平構造方程式が Matsuno (1966)が議論した 赤道β面上の浅水方程式と同形になるようにするために導入した.

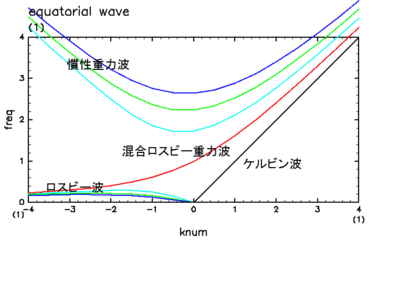
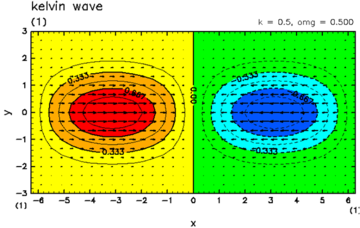
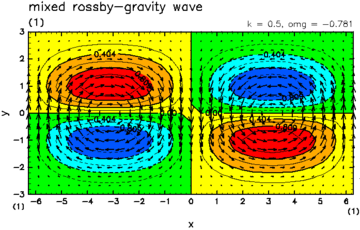
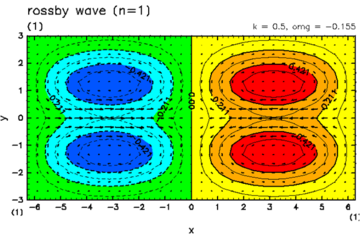
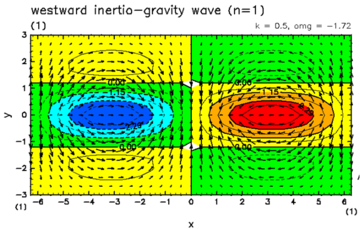
凝結加熱が無く(η=0), Hが正の実数である場合には, 赤道に振幅を持つ(y方向無限遠で振幅0となる)固有解として, 特定のHの値に対するモード解としては, 東進する一つのケルビン波, 一つのロスビー重力波, 西進する可算無限個のロスビー波, 可算無限個の慣性重力波が存在する (Matsuno, 1966). これらのモードの分散関係と重要ないくつかの水平構造を図A.1ならびに図A.2に示す.

図A.1: 赤道波の分散関係 波数(横軸)に対する振動数(縦軸)の表現.

図A.2: 赤道波の水平構造. (左上) ケルビン波, (右上) 混合重力波, (左下) ロスビー波, (右下) 重力波.

これらのうち本研究と最も直接に関連するのはケルビン波である. これは赤道上に U, V, P の最大振幅を持ち, 波数によらず一定の位相速度を持ち(すなわち非分散), その位相速度は等価深度から次のように与えられる.

赤道波 wave-CISK の問題に戻ろう. まず加熱の鉛直構造η(z)はある与えられた関数である. これを鉛直構造方程式に代入して適当な鉛直境界条件のもとで 固有値問題として解くことにより 一連の鉛直モード及び対応する固有値としての等価深度(分離定数)が得られ, この等価深度を水平構造方程式に代入することにより対応す る水平モードの分散関係と南北構造が定まる. したがって, 不安定モードの存否は鉛直構造方程式において 複素数の等価深度が存在するかどうかで判断することができる. ある鉛直モードの等価深度が複素数である場合, これに属する水平構造方程式の解は全て不安定となる.

どのような場合に複素等価深度が生じるかについては, 次節に簡単にまとめているが, 大まかに結論を記せば, 積雲による加熱が上空で強い(ηが上空で大きい)場合に 複素数の等価深度, したがって, 不安定擾乱が現れる.

不安定が余り強くない, すなわち, 等価深度の虚部の絶対値が実部の絶対値と比較して大きくない場合には, 不安定モードの水平構造は 上で述べた等価深度が実の浅水波方程式の場合と良く似た特徴を持つ. 一つの等価深度に対して, ケルビン波, 混合ロスビー重力波, ロスビー波, 慣性重力波に極めて良く似た解が存在し, それらの個数や分散関係(図A.3) そして南北構造も似通っている. ただし, 鉛直構造ならびに南北方向に位相の傾きを持つ点が重要な相違点である.

等価深度が複素数である場合, これに伴う鉛直固有モードは複素関数となる. これは, 擾乱の東西方向あるいは時間的な位相が高度によって異なることを意味する. 典型的には, wave-CISK 不安定擾乱は上空ほど位相が遅れた (赤道上を東進するケルビン波の場合, 西に傾いた)構造を持つ (図A.5).