F. 暴走温室状態の大気構造 |
 |
 |
 |
F. 暴走温室状態の大気構造 |
|
|
|
a. 全球平均値時間変化
これより暴走温室状態の熱力学的状態及び循環構造について 議論する. 実験 S1800 の結果を示していくことにする. 実験 S1600, S1700 に関しても時間が経過すれば同様な状態が 得られるものと考えられる.
| まず, 全球平均量の時間変化を見ることにする. 表面温度, OLRの全球平均値の時間変化を図 1 に示す. 全球平均入射量 450 W/m2に対して 1000 日の段階では全球平 均として 330 W/m2 程度しか射出できなくなる(図 1). このため大気は平衡状態に達することができず, 表面温度は時間とともに上昇していく. 1000 日の段階で表面温度の全球平均値は 360 K に達する(図 2). |
(a) 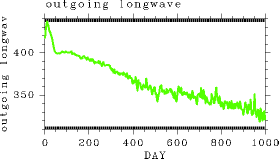 図 1: 実験 S1800 における OLR 全球平均値の時間変化. 単位は W/m2.
(b) |
| 暴走温室状態では,
温度の上昇が起こると同時に水蒸気量の増大も起こる.
大気中の水蒸気量をあらわす指標として潜熱エネルギーの時間変化の様子を
見てみる. 図 3
は全球平均潜熱エネルギーの時間変化を示したものである.
大気の潜熱エネルギーは単調に増加していき1000日の段階で 水蒸気量が増大する結果, 大気全量も時間とともに増加する. 表面気圧全球平均値の時間変化を図 4 に示す. 表面気圧も単調増加し, 1000 日の段階で 1230 hPa になる. 水蒸気量が増加するため大気が光学的に厚くなり射出するレベルは
|
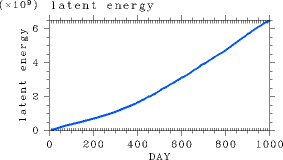
図 3: 実験 S1800 における潜熱エネルギーの全球平均値の時間変化. 単位は J/m2.
|
| 図 5 には降水量と蒸発量の全球平均値の時間変化を示した. 蒸発量は最初の500日までは単調に増加していき, それ以降はほぼ一定に 落ち着く. 降水量も増加していくが, 時間とともに変動も激しくなる. 蒸発量の大きさは日射量でほぼ決まってしまうのに対して (暴走温室状態の熱的南北構造で述べるように 入射エネルギーフラックスのほとんど全てが蒸発フラックスに変換される), 降水は不安定が発生した時点で大量に生じるようになったためであろう. 1000日の段階において降水量は蒸発量の 7 割程度になっており, 残りの約 3 割が大気中に蓄積されていくことになる. |
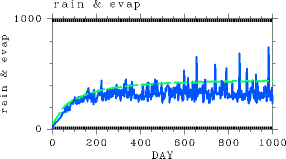 図 5: 実験 S1800 における蒸発量(緑線)と降水量(青線)の全球平均値の時間変化. 単位はどちらも W/m2. |
| 図 6 は運動エネルギーの全球平均値を示したものである. 大気の運動エネルギーは時間とともに減少する. この図は暴走温室状態においては循環強度が弱くなっていくことを示唆 している. |
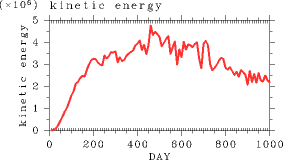
図 6: 実験 S1800 における運動エネルギーの全球平均値の時間変化. 単位は J/m2. |
| F.a. 全球平均値時間変化 | |
|
|
J/m2
となる. 
付近になる. また,
大気中の水蒸気量が非常に増加しているためその付近の温度構造は飽和
蒸気圧曲線で決まってしまうものとなる. そのため OLR
の値は水蒸気の飽和蒸気圧曲線で決まる温度構造によって決定
され,330 W/m2 に抑えられることになる. 