3. 結果

 3 次元灰色大気構造の太陽定数依存性と暴走温室状態 3.g. 暴走限界はどのようにして決まるのか？(成層圏モデルとの対応) 3.i. 暴走限界はどのように決まるのか？(放射対流平衡解による記述)

h. 暴走限界はどうのように決まるのか？
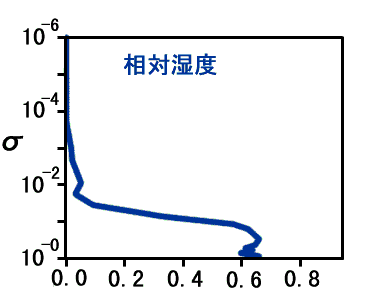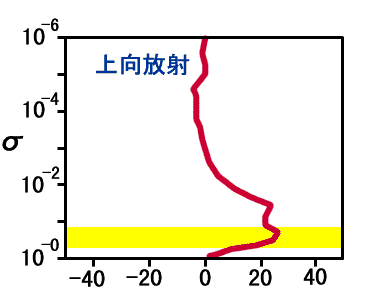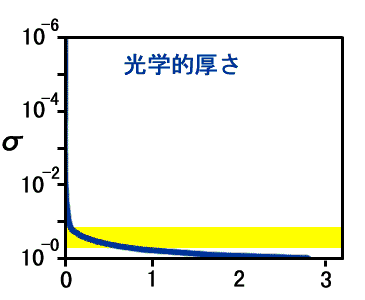
(鉛直構造の検討)

対流圏フラックス放出条件について考えるので, 暴走しないぎりぎりの状態である 実験 S1570 の場合の熱帯域の鉛直構造を詳しく見ていくことにする. 図 1 は温度, 相対湿度, OLR に対する各レベルからの寄与, 光学的深さの鉛直分布である. これらの図から以下の情報が得られる.

  • 相対湿度の鉛直分布
    対流圏中層まではおよそ 0.65, そこから等温層まで減少し, 0.1 となる. 対流圏全体で平均すると 約 0.6 となる.
  • OLR に対する各レベルからの寄与
    この図の曲線が最大となるレベル, つまり, log10σ = -0.5 (σ = 0.3)付近が OLR を決める上で最も重要で あることがわかる.
  • 光学的深さ分布
    OLR に対して主要な役割を果たす領域は τ=1〜0.1 に対応していることがわかる.
figure 1

図 1: 実験 S1570 の場合の緯度 2.77 における相対湿度, OLR に対する 各レベルの寄与(W/m2), 光学的厚さの鉛直分布. いずれも950 日から 1000 日の平均値. OLR に対する寄与とは, 各層から大気の上端まで到達する上向き放射 フラックスの大きさの分布を示したものである. この値が最も大きいレベルが OLR を決定する上で重要な役割を 果たしていると考えられる.

実験 S1570 における圏界面レベルは, 凝結加熱分布から判断するに σ=0.1 〜 0.2 である. 上の結果とあわせて考えれば, OLR の値は 対流圏の温度構造によって規定されているということがわかる. つまり, OLR の漸近値 400 W/m2 は 1 次元放射対流平衡解 における対流圏フラックス放出条件によって記述される可能性が ある. 次では, 1 次元放射対流平衡解の上限値と 3 次元計算で得られた OLR の漸近値との対応について考えることにする.

3.h. 暴走限界はどうのように決まるのか？
(鉛直構造の検討)		 3 次元灰色大気構造の太陽定数依存性と暴走温室状態 3.g. 暴走限界はどのようにして決まるのか？(成層圏モデルとの対応) 3.i. 暴走限界はどのように決まるのか？(放射対流平衡解による記述)