3. 結果

i. 暴走限界はどのように決まるのか？
(放射対流平衡解による記述)

以上の結果をもとに, 1 次元放射対流平衡解と 3 次元計算結果とを 比較してみることにする. ここで注意するべきことは, 3 次元の数値計算で得られた結果においては 相対湿度が 100 % になっていないという点である. Nakajima et al. (1992) で求められた 1 次元平衡解は 全て対流圏の相対湿度が 100 % であると仮定されていた. ここでは, 対流圏の相対湿度を 100 % とするのではなく, 3 次元計算で得られた値 60 % に固定した 1 次元放射対流平衡解を 考えることにする. 図 1 は 3 次元計算結果と 1 次元平衡解の鉛直温度構造を重ねて 書いたものである.   τ=1 となるレベル付近の温度構造は, ほとんど湿潤断熱温度勾 配で決まっていることがわかる. また, 相対湿度を 60 % に固定した場合の1 次元平衡解の OLR 上限値は 390 W/m² 程度になり (図 2), 3 次元系の暴走限界の値とほぼ一致する. 1 次元計算で OLR の上限値が存在するのは  τ=1付近の温度構造が断熱減率 で決まる構造になってしまうため対流圏上端における放射フラックスに上限が 存在するためである. 結局, 3 次元系の暴走限界は相対湿度を考慮した対流圏フラックス放出条件で 決まってしまうことになる.

図 1: 3 次元計算で得られた温度鉛直構造と大気下端温度から引いた 1 次元 放射対流平衡解の鉛直温度構造. 単位は W/m2.

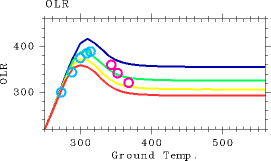
図 2: 表面温度(K)と OLR(W/m2) の関係. 曲線は様々な相対湿度を与えた場合の 1 次元放射対流平衡解 の結果. 赤線が相対湿度 100 %, 黄色線が 80 %, 緑色の線が 60 %, 青線が 40 % の場合. マークは, 3 次元計算で得られた全球平均表面温度と全球平均 OLR の関係. 青丸は 3 次元計算において平衡状態が得られた 場合の結果を, 赤丸は平衡状態が得られなかった場合の 1000 日 あるいは 2000 日の段階における結果を示す.

以上の考察によって, 3 次元世界においても 平衡解が射出する放射量には上限値が存在することが強く示唆される. したがって, 本研究の数値計算で得られた熱的な暴走状態は, Nakajima et al. (1992) によって 定義された暴走温室状態:平衡解が射出し得る放射量の上限値を超えた入射が 与えられた状態, に対応するものであることが正しく確認されたことに なる. この理由によって, S≧1600W/m² の場合に得られた熱的な暴走状態を暴走温室状態と呼んで良いということが 確認されたわけである.

3.i. 暴走限界はどのように決まるのか？ (放射対流平衡解による記述)