B. 1次元問題のまとめ

b. 1次元放射対流平衡解の性質

ここでは 1 次元放射対流平衡解が射出する放射量と平衡解の鉛直構造 について論じる.

1 次元放射対流平衡モデル

成層圏で q が一定の 1 次元放射対流平衡解を考える. 対流圏では湿潤断熱線によって, 温度構造・水蒸気量が決まるものと する. 1 次元放射対流平衡解は次の手順に従って求める.

1. 地表面温度 T_g を与える.
2. 地表面圧力 p_s を決める.
   p_s は T_g から次式によ って計算する.

   p_s = p_n0 + p^*_v (T_g).

   ここで,

   p_n0 は大気下端における乾燥空気(凝結性 成分) の分圧, p^*_v (T_g) は 温度 T_g における飽和水蒸気圧である. 水蒸気混合比 q を使って書くと
   $$p_s = P_n \times \{ 1 + q^* (T,p_n) \}$$

3. 地表から断熱線を引く.
   断熱条件を用いて地表(温度は T_g, 比湿は q^*(T_g) ) から出発して最上層まで 下から順に T_k 及び q_k = q^*(T_k) を決めていく.
4. 放射フラックスを計算する.
5. 圏界面圧力の近似値を求める.
   上層では放射フラックスがほとんど 一定となっており, そこでは放射平衡になっているものとし, 放射フラックスが減り始めるレベルがおおよそ圏界面に なっていると考えることにする.
6. 微調整.
   が正ならば更に下げる. つまり放射平衡になってるとした時の温度が, その場の温度よりも 高ければ下に下げる.
7. 圏界面を決定したら, その上(成層圏)は放射平衡にあるとして q 一定とおき, 温度を
   $$\sigma T^4 = \frac{F^{\uparrow}_{top}}{2} \left(\frac{3}{2} \tau + 1 \right)$$
   によって決める.
8. 再度放射フラックスを計算しなおす.

表面温度と OLR の関係

図 1 に 1 次元放射対流平衡モデルを用いて得られた 表面温度と OLR の関係を示す. この図には, 地表面における 非凝結性成分の分圧 pn0 として, 104, 105, 106, 107 Pa の 4 種類を与えた場合の結果を示してある. 図 1 では次のような特徴が現れている. どの場合でもOLR は最大値を持つ. 非凝結性成分量が増えるにしたがって OLR の最大値が増大し, 曲線が平らになる.

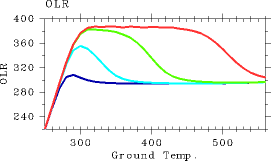
図 1: 1 次元放射対流平衡解の表面温度 (K) と OLR (W/m2) の関係. 青線は pn0=104 Pa , 水色の線は pn0=105 Pa, 緑線は pn0=106 Pa, 赤線は pn0=107 Pa の 場合の結果を示す.

まず, p_n0=10⁵ Pa の場合をもとに, 表面温度-OLR の関係についての考察を行うことにする. 詳細については, Nakajima et al. (1992) を参照されたい.

1. K の場合
   この場合, 大気の全光学的厚さは 1 を越えない. そのため, 上向きフラックスには地面放射 も大きく寄与する. よって, T_g が増加するほど OLR は増大する. しかし, 徐々に地面は見えなくなるのでOLR の増加のしかたはどんど ん鈍くなる.
2. K の場合
   となり, 圏界面における上向きフラックスは 主に対流圏中層の温度構造で決まる. 上向きフラックスの表式は
   
   であるので, OLR 付近の
   $$\DD{}{\tau'} \pi B = 4 \sigma T^3 \DD{T}{\tau'}$$
   で決まると考えられる. 従って, 付近の温度勾配が大きくなるほど OLR は大きくなる傾向にある. T_g が増大するにしたがって q が増加するので 温度勾配は湿潤断熱減率に近い値に漸近していく. このため, T_g が増大するに従って, OLR は減少する. OLR の値が 300 W/m² から 350 W/m² の間の場合, 平衡解が 2 つ存在している. これは, 温度の低い対流圏と地表面の組み合わせでも, 温度の高い対流圏だけでも, 同じ を射出でき るからである. 射出限界は, この場合 350 W/m² である. それは対流圏フラックス放出条件によって決まっている.
3. K の場合
   対流圏の水蒸気量が非常に増大するため温度構造は で決まるようになる. そのため, 付近の T の値 及びその勾配が T_g に依存しなくなるので, T_g の値によらず OLR の値が 1 つに決まってしまう. この場合, は対流圏中層の温度構造で決まる. 水蒸気が多量になった場合(飽和蒸気圧曲線で温度構造が決まる場合), は 305 W/m² 程度になり, W/m² となる.

以上より, 次の結論が得られる. 対流圏界面における上向き放射量に応じて, OLR の値 は定まる. ところが, 対流圏からの放射量は, 断熱条件によって定まる温度構造およ び水蒸気分布によって規定されているため, その値には上限値が存在する. したがって, OLR の値にも上限が存在することになる. この制約条件を本論文では, 対流圏フラックス放出条件 と呼ぶことにする.

次に, p_n0 が大きくなるに従って, OLR の最大値が増大し, 曲線は平になる傾 向について考える. p_n0 が増加すると乾燥空気の相対量が増えるので 温度勾配は乾燥断熱減 率に近い値になる. そのため, OLR は大きくなる. 実際, 計算結果を見てみると, 対流圏の温度構造と乾燥断熱温度構造とはほと んど差がなくなっている.

OLR が平らになってしまうのは次のような理由による. 光学的深さは
$$d \tau = k q \frac{dp}{g}$$
より,
$$\tau = \int^p_0 k q \frac{dp}{g}.$$
対流圏では温度構造が乾燥断熱減率で決まっているとすると
$$\DD{T}{p} = \frac{1}{\rho C_p}$$
これより成層圏の存在を無視すれば鉛直座標変数を T から p に 換えることができて
$$\tau = \int^p_0 k q \frac{1}{g} \rho c_p dT.$$
更に, 少ないながらも存在する水蒸気分布は, であるので,
$$\tau = \int^T_{T_{trop}} k p^{\ast} \frac{c_p}{g} dT.$$
となる. これを T について解くことができ,
$$\tau(T) = \frac{k p_0 c_p}{g R} \int^T_0 \exp \left( - \frac{L}{RT} \right) \frac{dT}{T}$$
となる. これより, τ を決めれば温度が一意的に定まってしまう. このため, 大気が光学的に厚く, T_g の寄与を無視することができるならば, OLR は T_g によらず 1 つの値になってしまう.

大気構造

以下では, 表面温度の値によって 1 次元放射対流平衡解の構造が どのように変化するかを見る. p_n0=10⁵ Pa の場合の結果を示すことにする.

温度の鉛直分布(図 2)を見てみると, T_g=300 K の場合で上層の温度がもっとも高くなる. これが, OLR の極大値に対応している. 比湿の値(図 3)は, 表面温度が増大するに従い全層に渡って 1 に近付く. 放射冷却が起こる領域(図 6)は, 表面温度が増大するにより上層に 位置するようになる.

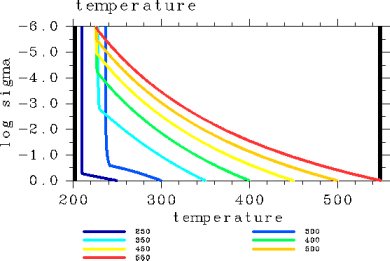
図 2: 温度鉛直分布. p_n0=10⁵ Pa の場合. 表面温度が250, 300, 350, 400, 450, 500, 550 K の場合. 単位は K.

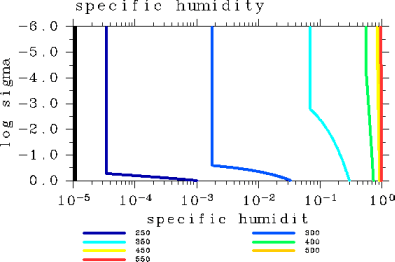
図 3: 比湿鉛直分布. p_n0=10⁵ Pa の場合. 表面温度が250, 300, 350, 400, 450, 500, 550 K の場合.

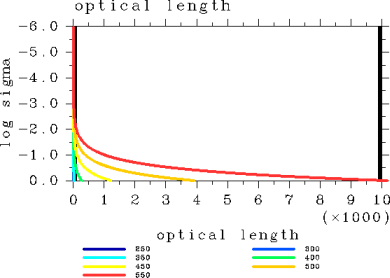
図 4: 光路長鉛直分布. p_n0=10⁵ Pa の場合. 表面温度が250, 300, 350, 400, 450, 500, 550 K の場合.

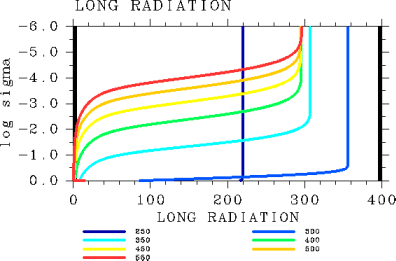
図 5: 正味上向き放射フラックス鉛直分布. p_n0=10⁵ Pa の場合. 表面温度が250, 300, 350, 400, 450, 500, 550 K の場合. 単位は W/m².

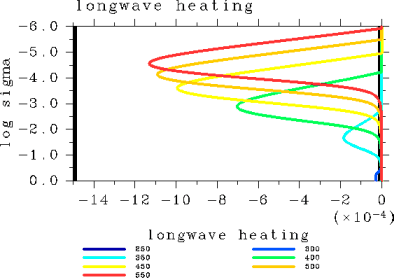
図 6: 放射加熱量鉛直分布. p_n0=10⁵ Pa の場合. 表面温度が250, 300, 350, 400, 450, 500, 550 K の場合. 単位は K/sec.

上で見てきたように表面温度が増加するに従い対流圏界面レベルは 高くなる. 表面温度と圏界面レベルの位置との関係を図 7 に示しておく. 表面温度が増大するに従い, 水蒸気量は増加するので大気量も増加する. 表面温度と表面気圧の関係を図 8 に示す.

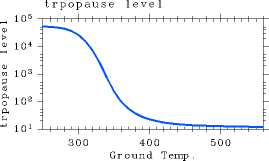
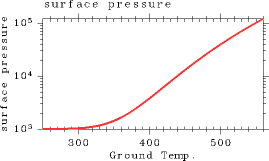
図 7: 圏界面圧力(Pa)の表面温度(K)依存性. pn0=105 Pa の場合. 図 8: 表面気圧(Pa)の表面温度(K)依存性. pn0=105 Pa の場合.

B.b. 1次元放射対流平衡解の性質