B. 1次元問題のまとめ

 3 次元灰色大気構造の太陽定数依存性と暴走温室状態 B.b. 1次元放射対流平衡解の性質 C.a. 基礎方程式

c. 放射量上限値の相対湿度依存性

ここまでは対流圏が飽和している場合を考えてきた. しかし, 3 次元計算への応用を考えると未飽和の場合についても議論しておく 必要がある.

相対湿度を考慮した場合のKomabayashi-Ingersoll 限界

　

成層圏では水蒸気の比湿が一定である, 対流圏界面が 未飽和である場合は,
displaymath6212

displaymath6213
が成り立つ. ここで, RH は相対湿度である.

これより F^{\uparrow}_{top} について解くと
displaymath6214
となる. この式を用いて tex2html_wrap_inline6222 の最大値を求めた結果を図 1に示す. 図からわかるように, 相対湿度が減少すれば tex2html_wrap_inline6222 は急激に 増大する. 特に, tex2html_wrap_inline6226 の場合では, tex2html_wrap_inline6228 W/m2 になる.

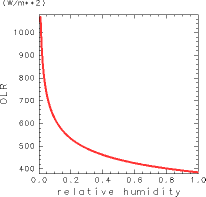
figure1
図 1: 対流圏界面の相対湿度を考慮した時の成層圏の射出限界.

放射対流平衡解の最大射出量

　

1 次元放射対流平衡モデルにおいて相対湿度を考慮した場合に 放射量の最大値がどのように変化するかを調べる. そのため, 平衡解を求める際, まず断熱線を引いてから指定された 相対湿度の値だけ水蒸気を減らし放射計算を行なうことにした. このようにして相対湿度の値を様々に固定して求めた 表面温度と OLR の関係を図 2 に示す. 相対湿度が低くなるにつれ, 最大射出量も高温極限における漸近値も 大きくなる. 相対湿度が 60 % の場合には, 最大射出量は 390 W/m2 に, 高温極限での漸近値は 320 W/m2 となる.

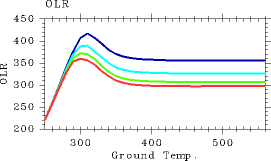
 figure2
図 2: 相対湿度を変化させた場合に 1 次元放射対流平衡モデル で得られる表面温度(K)とOLR (W/m2)の関係. 赤線が相対湿度 100 %(Nakajima et al., 1992 の同一の場合), 緑線が 80 %, 水色の線が 60 %, 青線が 40 % の場合.
B.c. 放射量上限値の相対湿度依存性 3 次元灰色大気構造の太陽定数依存性と暴走温室状態 B.b. 1次元放射対流平衡解の性質 C.a. 基礎方程式