B. 1次元問題のまとめ

a. 放射平衡解の性質:成層圏モデルの結果

成層圏モデル

Kombayashi (1967), Ingersoll (1969) と同様の成層圏モデルを考える. 成層圏は放射平衡解になっているので, 構造は次の 3 式で決定される.

, はそれぞれ, τ を鉛直座標としたときの上向き放射フラックス, 下向き放射フラックス, である. $F^{\uparrow}_{top}$ が OLR に対応する. その他の変数・パラメータの定義に関しては, 基礎方程式を参照して頂きたい.

更に, 平衡解を決定するため成層圏の下端は飽和していることを要請する. その根拠は成層圏の下端は対流圏界面に相当し湿潤断熱線上に乗っていると考えるからである. 今, 成層圏では q が一定となる場合を考えているので

となる. 従ってこのモデルでは τ の値によって水蒸気量が一意に決まってしまう.

上式で定まる水蒸気分布をもとに露点温度の分布を求めることにする. 放射フラックスの表式と同様に τ の関数として表す. 飽和蒸気圧曲線

を, τ の定義式を用いて書き換えると

が得られる.

平衡解の存在条件

上記のモデルでは対流圏界面の位置が決まれば平衡解が決まることになる. $\sigma T^{4*}(\tau)$ と放射平衡解ののグラフが重なった点が対流圏界面である. 図には, 露点温度分布 $\sigma T^{4*}(\tau)$ と 3 種類の $F^{\uparrow}_{top}$ を与えた場合の放射フラックスの分布を示す.
これらの図から以下の結論が得られる.

W/m² の場合
平衡解が 2 つ存在する. このうち, 対流圏界面が高いレベルに位置する解は物理的に意味がない. 成層圏において過飽和の領域が存在するからである.

W/m²の場合
平衡解が 1 つだけ存在する.

W/m² の場合
平衡解は存在しない.

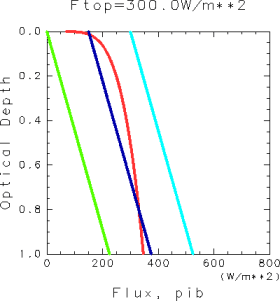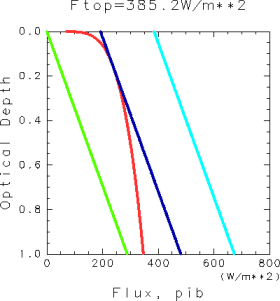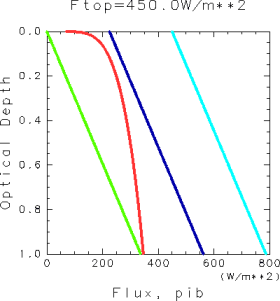
図 1: 放射平衡解と露点温度の鉛直構造. 赤線が露点温度から決まる $\sigma T^{4*}(\tau)$ , 水色の線が上向き放射フラックス , 青線が放射源関数 , 緑色の線が下向き放射フラックスを表す. 重力定数 g を 9.8 ms^-2, 水蒸気の吸収係数 $\kappa$ を 0.01m²Kg^-1とした場合の結果である.

以上より, 成層圏モデルにおいて平衡解が存在するためには次の条件を満たされていなければならないことがわかる. $\pi B(\tau)$ のグラフと $\sigma T^{\ast 4}(\tau)$ のグラフが交点を持たねばならない. 上で用いたパラメータ値の場合, この条件は

となる.

この条件は, Komabayashi (1967), Ingersoll (1969) により求められた. 本論文では圏界面フラックス通過条件と呼ぶことにする. また, この条件によって定まる放射量の上限値を Nakajima et al. (1992) に習って Komabayashi-Ingersoll 限界と呼ぶことにする.

B.a. 放射平衡解の性質:成層圏モデルの結果