A. 暴走温室状態の研究年表

 3 次元灰色大気構造の太陽定数依存性と暴走温室状態 3 次元灰色大気構造の太陽定数依存性と暴走温室状態 B.a. 放射平衡解の性質:成層圏モデルの結果


暴走温室状態の研究年表

Simpson(1927)

動機
気候の安定性
概要
飽和蒸気圧曲線の関数形をもとにした定性的な議論.
結果
大気が射出できる放射量には上限値が存在することを示唆した.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Plass(1961)

動機
金星大気あるいは地球大気の進化の考察.
概要
温度の上昇と蒸発のフィードバックに関する考察.
結果
水蒸気量の増加と気温上昇の間には正のフィードバックが存在することを 指摘した.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Gold(1964)

動機
金星大気あるいは地球大気の進化の考察.
概要
温度の上昇と蒸発のフィードバックに関する考察.
結果
水蒸気量の増加と気温上昇の間には正のフィードバックが存在することを 指摘し, 暴走的に温度が上昇してく状態が存在する可能性を示唆した.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Komabayashi (1967)

動機
気候の安定性
モデル
灰色成層圏モデル
結果
下端で飽和した成層圏が射出できる放射量には上限値が存在することを 定量的に示した. 議論の詳細については, 放射平衡解の性質:成層圏モデルの結果 を参照のこと.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Ingersoll (1969)

動機
金星大気の進化
過去の金星は暴走温室状態にあり水蒸気が大気中 に留まっていたため, 大気上層における水蒸気の光分解, 水素の消散が進み 現在の金星大気が形成された, と考える.
モデル
灰色成層圏モデル
結果
下端で飽和した成層圏が射出できる放射量には上限値が存在することを 定量的に示した. 放射量の上限値を超えた入射フラックスが与えられた状態を 暴走温室状態と呼んだ. 過去の金星において暴走温室状態が発生した可能性を示唆した. 議論の詳細については, 放射平衡解の性質:成層圏モデルの結果 を参照のこと.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Rasool and deBergh (1970)

動機
金星大気の進化.
モデル
1 次元放射対流平衡モデル.
結果
過去の金星において暴走温室状態が発生したと議論した.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Pollack (1971)

動機
金星大気の進化.
モデル
1 次元放射対流平衡モデル. 非灰色大気.
結果
現在の金星では大気海洋系は平衡に達することができないこと, 暴走温室状態にあることを示した.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Lindzen et al. (1982)

動機
積雲対流の効果に関する考察.
モデル
1 次元放射対流平衡モデル. ただし, 彼らのモデルには幾つか欠点があることが指摘されている. 例えば, 放射スキームで計算される放射量は黒体放射以上の大きさ になる場合がある.
結果
積雲対流の効果によっては暴走温室状態が発生しないと結論した.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Vardavas and Carver (1985)

動機
積雲対流の効果に関する考察.
モデル
1 次元放射対流平衡モデル.
結果
積雲パラメタリゼーションスキームあるいは相対湿度の値によって 暴走温室状態が発生する入射エネルギーフラックスの値がどの程度 違ってくるかを調べた.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Abe and Matsui (1988)

動機
地球型惑星の形成期には, 激しい微惑星衝突のため水蒸気などの揮発性成分が 脱ガスし原始大気が存在していた(Abe and Matsui, 1985 など). Abe and Matsui (1988) は, 地球型惑星の初期進化及び海洋の形成過程 に関して考察を行うため原始大気の構造を求めた.
モデル
1 次元放射対流平衡モデル. 非灰色, 気体の非理想性も考慮.
結果
入射エネルギーフラックスが約 300 W/m2を超えると海洋が存 在できないことを示した. このため, 海洋は存在できず, 数百気圧の厚い大気が原始惑星を覆っていたと考えられる. 微惑星衝突の頻度が減少する惑星形成末期には大気 へのエネルギー供給量も減少し, 海洋が形成されることになる.


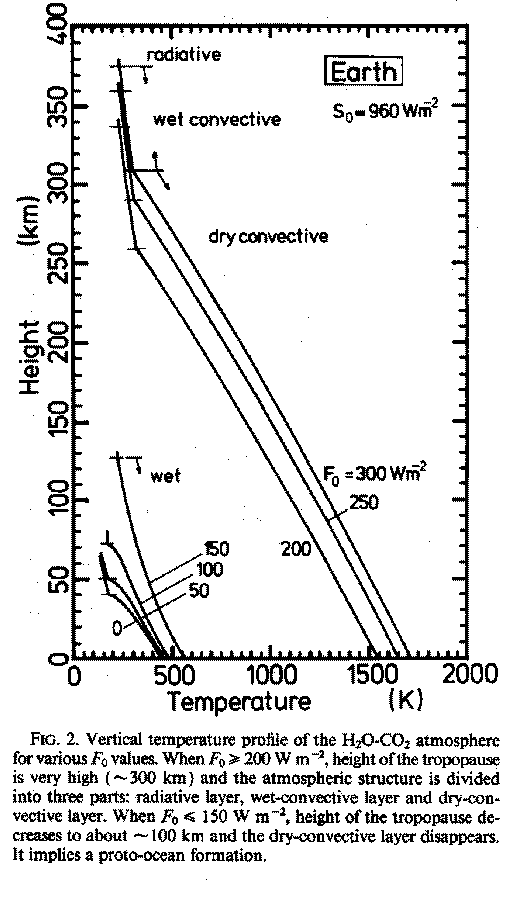
figure 1
図 1: Abe and Matsui (1988) の Figure 2. 入射エネルギーフラックスの値によって 大気構造が大きく変化することが示されている.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Kasting (1988)

動機
地球型惑星の初期進化.
モデル
1 次元放射対流平衡モデル.
結果
大気に与えられるエネルギーフラックスが現在の 地球にお ける太陽定数の1.4 倍になると暴走温室状態が引き起こされるという 結論を得た.

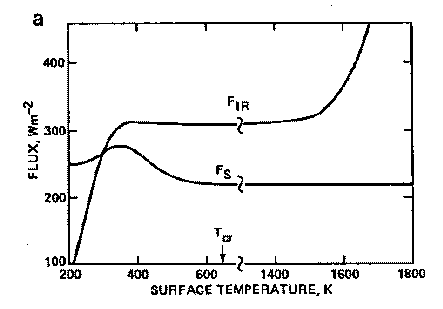
figure 2
図 2: Kasting (1988) の Figure 7a. 表面温度と 外向き赤外放射 F_IRの関係が示されている. 表面温度が 1500 K に上昇しても赤外放射量は 300 W/m2 程度を超えられない.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Nakajima et al. (1992)

目的
暴走温室状態の概念の整理.
モデル
1 次元放射対流平衡モデル
結果
大気が射出する放射量には以下のような制約条件が存在することを 示した.
  • 大気の外向き放射量は Komabayashi-Ingersoll 限界 (成層圏モデルにおける射出放射量の上限値) を超えられない. 地球的なパラメータのもとでは, Komabayashi-Ingersoll 限界は 385 W/m2 になる.
  • 高温状態における大気の外向き放射量は, 水蒸気大気が 射出する放射量以上となる. 水蒸気大気の放射上限値は, 対流圏界面における上向き 放射フラックスの上限値によって規定されている. 水蒸気大気の放射上限値は, 地球的なパラメータの値では 300 W/m2)となる.

更に, 対流圏界面における上向き放射量の最大値は対流圏の温度構造 によって定まることも示された. 実際に大気が射出できる放射量の上限値は, 対流圏界面の放射フラックスの上限値によって定まる値 と Komabayashi-Ingersoll 限界との大小関係によって 定まることになる. 乾燥空気量や比熱の値などを地球に近いものに選ぶと 大気が射出できる放射量の最大値は 350 W/m2となる. Abe and Matsui (1988) および Kasting (1988) が得た海洋が平衡解消失点は対流圏の温度構造に よって規定される射出限界の値に対応していることも示された.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Renno et al. (1995)

目的
積雲対流の取り扱い方によって暴走温室状態の発生条件が どの程度変化するかを調べる.
モデル
1 次元時間発展モデル. 対流調節等 6 種類の積雲パラメタリゼーションスキームを使用.
結果
相対湿度の値がある程度大きいものであれば積雲パラメタリゼーション スキームによらず熱的な暴走状態が発生する. 彼らは, この熱的な暴走状態を暴走温室状態と呼んでいる. しかし, 1 次元放射対流平衡モデルにおける放射量上限値 と暴走温室状態が発生する入射放射量との関係は何も 議論されていない.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

Pierrerhumbert (1995)

目的
大気の平衡状態に関する考察.
モデル
暴走温室状態が発生している領域と発生していない領域 を考えたボックスモデル.
結果
暴走温室状態が発生している領域から発生していない領域 に熱輸送が起こることにより大気の平衡状態が実現されているという アイディアを示した.

[暴走温室状態に関する過去の研究(本文)に戻る] [年表] [目次]

A. 暴走温室状態の研究年表 3 次元灰色大気構造の太陽定数依存性と暴走温室状態 3 次元灰色大気構造の太陽定数依存性と暴走温室状態 B.a. 放射平衡解の性質:成層圏モデルの結果