C. モデルの詳細

 3 次元灰色大気構造の太陽定数依存性と暴走温室状態 C.b. 放射計算スキーム C.d. 蒸発・凝結による表面気圧変化

c. 鉛直分解能についての検討

ここでは放射計算に必要な鉛直分解能についての検討を行なう. 種々の鉛直分解能を用いた 1 次元計算の結果を比較することにより 放射計算にとって最低限必要な鉛直分解能を見極める.

鉛直レベルの位置

　

Nakajima et al. (1992) では 1 次元放射平衡解を求めるために 鉛直層数が 400 〜 700 の計算を行なっている. しかし, 3 次元時間発展問題をそのような高分解能で行なうことは実質的に 不可能である. 3 次元計算を行なうためには, 放射計算を十分に精度良く行なえる最低限の 鉛直層数を見いだす必要がある. そのため, ここでは鉛直層数が 16, 21, 32, 1000 の 4 つの場合の比較を 行なうことにする. それぞれの鉛直層数をとったモデルを, L16, L21, L32, L1000 と呼ぶことに する. L32 におけるレベルの位置を表 1 に示す.

L16における鉛直レベルは15層までは 表 1 に示されたものと同じレベルを用い 16層目を0にとる. L21 の場合, L16 のものに σ=10-1, 10-2, 10-3, 10-4, 10-5 を加える. L1000 の場合では, 全層(tex2html_wrap_inline6408 から 10-6)を tex2html_wrap_inline6670 で等間隔に分割する.

ちなみに, Nakajima et al. (1992) では全層を tex2html_wrap_inline6670 で 等間隔に分割して計算を行なっている. 層の数は
\begin{displaymath} NNL = \frac{p_{bottom} - p_{top}}{\ln 10 /100} + 1\end{displaymath}
とする. 実際の層の数は, Cpv = 4 R, Cpn=3.5 R, Pn0=105 Pa, Tg = 500 K の場合で 560 層, Cpv = 4 R, Cpn=4.5 R, Pn0=108 Pa, Tg = 500 K の場合で 702 層である.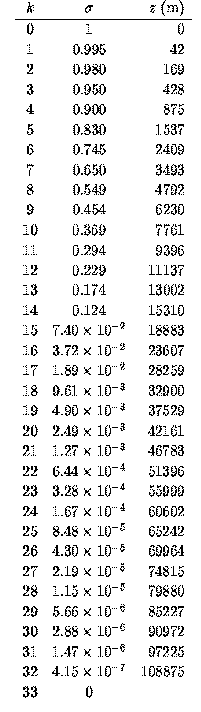

table1043
表 1: 鉛直格子の位置. k は鉛直格子番号. 地表面から順に 0, 1, 2,… とする. σはσ座標値. z は S=1380 W/m2 の場合に得られた ジオポテンシャル高度の全球平均値(m).

Tg-OLR 関係

ここでは種々の鉛直分解能を用いた場合に, Tg と OLR の関係が正しく得 られるかどうかを調べる.

pn0=105 Pa とした場合について 種々の分解能を用いて, 表面温度と OLR の関係を求めたものを 図 1 に示す.

　

L32 の場合における OLR の Tg 依存性は L1000 と同様になった. しかし, L21 に分解能を下げると Tg - OLR 曲線がガタガタになってしまう. この場合, 対流圏界面レベルを正確に求めることができないため 正しい放射フラックスの値を計算することができなくなってしまっている. 更に鉛直分解能を下げ, L16 とするとOLR の平らな領域があらわれない. このような結果になった理由は, Tg が350 K を越えた高温状態では, 対流圏がモデル領域をつきぬけてしまうためである. L16 の場合, 最上層レベルは $\sigma=0.05$ であるが, Tg が350 K を超えると対流圏界面のレベルはこれよりも高くなってしまうのである.

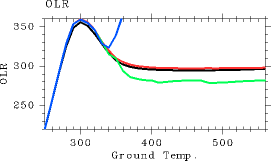
figure1
図 1: C_{delta tau}=0.1 の場合の表面温度 (K) と OLR (W/m2) の関係. pn0=105 Pa の場合. 黒線が L1000 の結果を, 赤線が L32 を, 緑色の線が L21 の結果を, 青線が L16 の結果を表す.

L32 の場合と L1000 の場合で実際の数値を比較するため, Tg - OLR 曲線の裾野付近の OLR の値と ピーク付近の値を, それぞれ表 2 と表 3 に示す. L1000 と L32 との差はせいぜい 5 W/m2 に留まっている. よって, L32 であれば放射計算は 5 W/m2 の精度で行なう ことができると考えられる.

table2
表 2: 表面温度-OLR グラフにおける裾野付近の OLR の値. L1000 は鉛直レベル数を 1000 とした場合に得られる OLR の値. L32 は鉛直レベル数を 32 とした場合に得られる OLR の値. 単位は W/m2.

table3 表 3: 表面温度-OLR グラフにおける「山」付近の OLR の値. L1000 は鉛直レベル数を 1000 とした場合に得られる OLR の値. L32 は鉛直レベル数を 32 とした場合に得られる OLR の値. 単位は W/m2.

　

以上で pn0 が 105 Pa の場合には L32 で 十分精度良く OLR を計算可能であることが示された. 次に, L32 において地表面における非凝結性成分の分圧を変化させた場合に 正しく 1 次元平衡解を求めることができるのかどうか調べることにする. 地表面における非凝結性成分の分圧 pn0 を, 104, 105, 106,107 Pa と変えた場合に L32 を用いて求めた Tg-OLR 関係を 図 1 に示す. L32 でも Pn0 = 105 Pa までなら L1000 と非常に良く似た結果を与え ることがわかる. しかし, Pn0 = 106 Pa になると曲線に凸凹が目立ち始め, Pn0=107 Pa の場合では山の上の方でガタガタになる. いずれの場合でも, L1000 とした場合に比べてL32 の方がOLR の値が大きくなっ ている. 特に, pn0 = 107 Pa の場合には, Komabayashi-Ingersoll 限界 (385 W/m2) すら越えてしまっている. L32 の場合, pn0 = 106 Pa 程度までであれば OLR の値は 正しく計算で きる, と思われる.

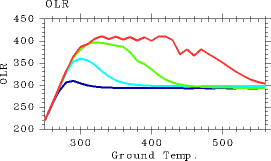
figure2
図 2: 種々の非凝結性成分量を与えた時の 表面温度(K) と OLR (W/m2) の関係. 青線は pn0 = 104 Pa, 水色線は pn0 = 105 Pa, 緑線は pn0 = 106 Pa, 赤線は pn0 = 107 Pa の場合. 鉛直分解能は L32.

鉛直構造

L32 であれば, pn0 < 106 Pa の場合に OLR の値は正しく計算できるこ とは確認された. ここでは, L32 で物理量の鉛直分布も L1000 と同様の結果を与えるかどうか見てみる. 図 3, 4 に温度の鉛直分布と正味上向き放射フラックスの鉛直分布 を示した. いずれも L1000 の結果と同様の分布を示しており, 鉛直構造も L32 で十分計算できることが確認された.

結論として, このスキームを用いて pn0 = 105 Pa, $T_g \le 560$ K の状態を計算するのであれば, L32 で十分であると考えられる.

(a) 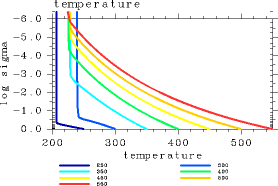figure1(a) (b) figure1(b)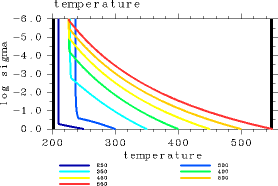


図 3: 1 次元平衡解の温度鉛直分布. (a): L32 の場合. (b) L1000 の場合. pn0=105 Pa. Tg = 250, 300, 350, 400, 450, 500, 550 K の場合 の結果を示してある. 単位はいずれも K.

(a) 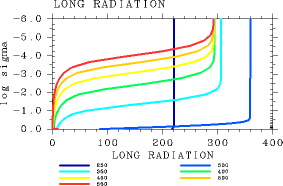figure4(a) (b) figure4(b)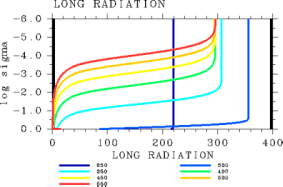


図 4: 1 次元平衡解の正味上向き放射フラックス鉛直分布. (a): L32 の場合. (b) L1000 の場合. C_{delta tau}=0.1 Pa. pn0 = 105 Pa の場合. Tg = 250, 300, 350, 400, 450, 500, 550 K の 場合の結果を示してある. 単位はいずれも W/m2.

まとめ

放射計算に関しては, pn0＜106 Pa であれば 鉛直層数は 32 で十分である. ただし, この結果は1 次元平衡解を求める上での放射計算にとって 最低限必要な鉛直層数であるに過ぎない. 力学計算にとってはこれで十分であるかどうかについては別の検討を要する. これは今後の課題である.

C.c. 鉛直分解能についての検討 3 次元灰色大気構造の太陽定数依存性と暴走温室状態 C.b. 放射計算スキーム C.d. 蒸発・凝結による表面気圧変化