C. モデルの詳細

 3 次元灰色大気構造の太陽定数依存性と暴走温室状態 C.a. 基礎方程式 C.c. 鉛直分解能についての検討

b. 放射計算スキーム

ここでは数値計算に用いる放射スキームとその特性について解説を行う. ポイントは, 放射フラックスの式を2通りに差分化しそれをつなげることである. これにより任意の光学的深さ分布を持つ灰色大気の放射計算を行なうことができる.

放射フラックスの差分表現

灰色大気の場合の正味上向き放射フラックスは次式で与えられる.
\begin{eqnarray*} F^{net} (\tau) & = & \pi B(\tau_{top}) e^{-(\tau-\tau_{top})... ...{\tau'} d e^{-(\tau-\tau')} \Deqlab{net rad flux:cont:modify}\end{eqnarray*}
$\tau_{top}$ は大気の上端における光学的深さであり, $\tau_{top}=0$ とする. πB は σT4 である.

ここでは Nakajima et al. (1992) と同様にして 放射フラックスの式を次のように差分化する
\begin{eqnarray*} \Deqlab{net rad flux:discret} & & F^{net} (k+\frac{1}{2} ) =... ...au_{j+\frac{1}{2}} \geq C_{\Delta \tau} ) \end{array} \right. \end{eqnarray*}
KMAX は最上層レベルであり, 標準的な場合では KMAX=32 である. 放射フラックスは, この 2 種の差分式をつなげて計算することにし, 光学的に薄い層からの寄与は上の段の式を, 光学的に厚い層からの寄与は 下の段の式を用いて積分を評価する. tex2html_wrap_inline6452 の値によって上の段と下の段の使われ方の 割合が変わってくる. tex2html_wrap_inline6452 の値を非常に大きなものにとれば, 積分の評価は全 て上の式を用いて行なわれることになり, Numaguti and Hayashi (1991) で使用されている放射スキームと対応するものになる.

なお, 上の段の式と下の段の式が等しくなるような tex2html_wrap_inline6474 は 存在しない. 仮にそのような tex2html_wrap_inline6474 があったとすると
\begin{eqnarray*} & & \frac{\pi B(j-\frac{1}{2}) - \pi B(j+\frac{1}{2})} {\tau_... ... } + e^{-(\tau_{k+\frac{1}{2}} - \tau_{j+\frac{1}{2}}) }} { 2 }\end{eqnarray*}
が成立しなければならない. tex2html_wrap_inline6478 とおいて, この条件を整理すると
\begin{displaymath} \frac{1 - e^{\Delta \tau} }{\Delta \tau} = \frac{1 + e^{\Delta \tau} }{2} \end{displaymath}
が得られる. 残念ながら, この式の解は存在せず, 正確にはスキームをつなげかえるレベル ではフラックスの評価に不連続が生じてしまう. しかし実際にはその差はほとんど無視できるほどに小さい. 放射フラックスの鉛直分布 (1 次元放射対流平衡解の性質, 図 4 参照) においても不連続性は見えない.

このように複雑なことを行なう理由は, 放射フラックスの差分式の上 の段の差分式だけを用いた場合でも, 下の段の差分式だけを用いた場合でも不 都合が生じるからである. その理由を以下に示し, それにより3次元計算で用いるtex2html_wrap_inline6452の値 についての検討を行なう.

CΔτ を大きくした場合

　

まず, tex2html_wrap_inline6452 を非常に大きくした極限を考える. これは, 放射フラックスの差分式において全層に渡って上の段の式を 用いること, すなわち Numaguti and Hayashi (1991) の放射スキームを用い ることに対応する. 例として, tex2html_wrap_inline6494, Pn0 = 105, 鉛直分解能を L1000 とした場合の結果を示す. Tg と OLR の関係は tex2html_wrap_inline6526 の場合とほとんど 同様の結果を与える(図は示さない). しかし, 高温状態における放射フラックスの鉛直分布は正しく計算されていな い. 図 1 に Tg=550 K の場合の正味上向き 放射フラックス鉛直分布を示す. tex2html_wrap_inline6526 の場合とは異なり, $\log_{10} \sigma = -2$ 付近から下では正味上向きフラックスが地表に近付くほど増加している. 正味上向きフラックスが中層で上から下に向かって増加しあるレベルから再び 上から下に向かって減少する. この理由は, 光学的に厚くなった場合, 放射フラックスの差分式の下 段の式において j=k のところしか残らず, 正味上向きフラックスが
displaymath6482
と評価されてしまうからである. 正しくは,
displaymath6483
となるべきである.

(a) 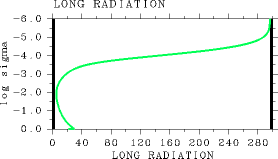figure35

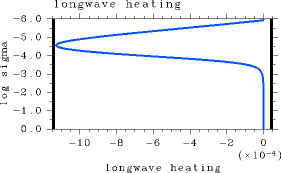
(b) figure35
図 1: tex2html_wrap_inline6494 の場合の結果. L1000, pn0=105 Pa, Ts= 550 K の場合. (a): 正味上向き放射フラックス鉛直分布. 単位は W/m2. (b): 放射加熱率鉛直分布. 単位は K/sec.

この計算における, tex2html_wrap_inline6506 及び正味上向き放射フラックスの値は
displaymath6484

displaymath6485
となっている.

　

L32 の場合では上記のことがもっと激しく起こる. 正味上向き放射フラックスは, $\log_{10} \sigma = -3$ 付近から下に向かっ て増加するが, $\log_{10} \sigma = -1$ 付近から再び減少する(図 2a). この場合も $\log_{10} \sigma = -3.0$ 以下では正味上向き放射フラックスが $\sigma T^4_{k-1} - \sigma T^4_{k}$ で決まってしまうためにこのようなこ とが起こっている. 地表付近で減少する理由は鉛直格子点間隔が狭くなるためである. $C_{\Delta \tau}=10^6$ の場合に おける $\log_{10} \sigma = -1$ 付近でのフラックスの値は $C_{\Delta \tau}=10^{-1}$ の場合に おける値よりも 400 W/m2 も大きくなっている. $C_{\Delta \tau}=0.1$ の場合に比べて, 上向きフラックス, 下向きフラック スともに中層で 200 W/m2 程度の差が生じている. 3 次元の時間発展問題において問題となるのは放射加熱量の分布であるが, これについてはそれほど誤差は目立たなくなっている(図 2b).

(a) 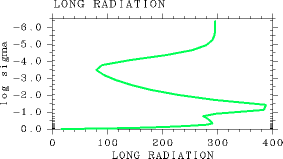figure35

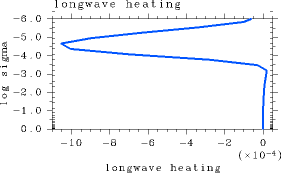
(b) figure35
図 2: tex2html_wrap_inline6494 の場合の結果. L32, pn0=105 Pa, Ts= 550 K の場合. (a): 正味上向き放射フラックス鉛直分布. 単位は W/m2. (b): 放射加熱率鉛直分布. 単位は K/sec.

L32 の場合では $C_{\Delta \tau} \geq 10.0$ の場合に中層で放射フラック スの鉛直分布に不連続が生じるようになる. 図は示さないが, L32 では, $C_{\Delta \tau} \leq 1.0$ であればほとんど 問題なく放射フラックスの計算が可能である.

CΔτ を小さくした場合

　

tex2html_wrap_inline6452 を非常に小さくした極限では結果がどのようになるかを見る. これは, 放射フラックスの積分を 全層に渡って差分式の下の段の式によって評価することに対応する. 例として, $C_{\Delta \tau} = 0.0$, Pn0 = 105, 鉛直分解能は L32 とした場合の結果を示す. この場合, 1 次元放射対流平衡計算の手順に従い 1 次元平衡解を求めた場合の最 終的な正味上向きフラックスは一見正しく計算されているように見える(図は 示さない). しかし, Tg=250 K の場合, 下から上まで断熱線を引いた状態の放射計算は 正しく行うことができない. 上向きフラックス, 下向きフラックスはそれぞれ 図 3 ので示すように不連続が生じてしまう. ちなみに, Tg=300 K 程度までこのような不連続が明瞭に見える. この原因は, 光学的に薄い領域, つまり低温状態の上層では,
\begin{displaymath} \Deqlab{de/dtau} \Deqlab{de/dTau} \DD{e^{-\tau}}{\tau} \r... ...\frac{1}{2}} )} }{\tau_{j-\frac{1}{2}} - \tau_{j+\frac{1}{2}}}\end{displaymath}
が 0 になってしまうことにある. このスキームを用いた場合, $\tau_{j-\frac{1}{2}}$, $\tau_{j+\frac{1}{2}}$ の値が非常に小さくなるので数値上の誤差範囲内で $e^{-(\tau_{j-\frac{1}{2}}-\tau_{k+\frac{1}{2}} )}$ と $e^{-(\tau_{j+\frac{1}{2}}-\tau_{k+\frac{1}{2}} )}$ はともに等しい値に 計算されて, その差が 0 と評価されてしまうのである. 本来ならば, $d e^{-\tau}$ と $d \tau$ がともに非常に小さくなり
\begin{displaymath} \DD{e^{-\tau}}{\tau} \sim 1\end{displaymath}
となるはずである. displaymath6548 が 0 になってしまうレベルより上の下向きフラック スは
\begin{displaymath} - \pi B(K_{MAX} + 1) e^{-(\tau_k - \tau_{K_{MAX}+1})} + \pi B(k)\end{displaymath}
で決まってしまうため, 正確な値よりも小さくなる. 上向きフラックスの場合も同様で, displaymath6548 が 0 になるレベルより上においては和の項のいくつかが落ちてしまう.

(a) 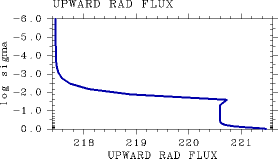figure3(a)
(b)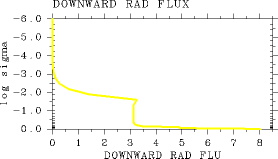 figure3(b)
図 3: $C_{\Delta \tau} = 0.0$ とした時に 大気最下層から断熱線を引いた状態で計算される (a): 上向き放射フラックス鉛直分布と (b): 下向き放射フラック ス鉛直分布. L32, pn0=105 Pa, Ts= 250 K の場合. 単位はいずれも W/m2.

なお, 鉛直分解能を上げるともっと極端に上記の不具合が発現する. L1000 の場合では OLR の値も正しく計算できなくなり, 正しく Tg と OLRの関係が求められなくなる(図は示さない).

結論としては, 大気の全層に渡って差分式の上の段の式を用いることはできない. しかし, $C_{\Delta \tau} \geq 10^{-7}$ であれば, 問題なく放射フラックスを計算できることは確認されている(図は示さない).

まとめ

放射フラックスの差分式の上の段の式だけを用いると光学的に薄い大 気の放射計算において不都合が生じる. また, 下の段の差分式だけでは光学的に厚い大気の放射計算はできない. しかし, 2 種の差分式を組み合わせることにより任意の光学的深さ分布を持つ 灰色大気の放射計算が可能である. その際, 差分式のつなぎ変えを規定する CΔτ の値は 1.0 から 10-7 の間にとらなければならない. 以上の結果をもとに, 本論文では CΔτ の値として 0.1 を採用することにする.

C.b. 放射計算スキーム 3 次元灰色大気構造の太陽定数依存性と暴走温室状態 C.a. 基礎方程式 C.c. 鉛直分解能についての検討