2.2 コンターダイナミクスの定式化
Dritschel(1989)
をもとに、 コンターダイナミクスの基本をまとめておく。渦度の分布 Q (x,y,t ) から流線関数
ψ(x,y,t ) を求めるには、
(2.3)
を解けばよい。これはポアッソン方程式で、一般解はグリーン関数を用いて
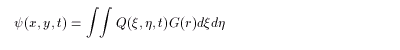(2.4)
で与えられる。ただし
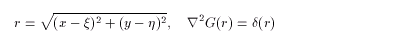(2.5)
2次元の無限平面の場合、グリーン関数は G (r
) = ( log r )/ 2π なので、
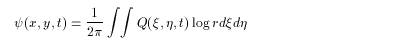(2.6)
である。速度 (u,v ) は次のようになる。
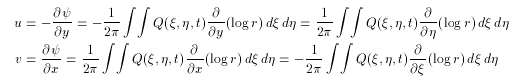(2.7)
式(2.7)で、ηで部分積分をおこなうと、
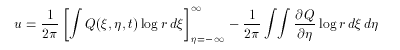(2.8)
右辺第2項の積分の中身はコンター上でのみ値をもち、ηで積分した値は
渦度のジャンプ q ( j )
と等しい。 q ( j )
を、コンター Cj
を内側に横切ったときの
渦度ジャンプとし、線積分を反時計回りにすると、
(2.9)
となる。v
についても以上のことを同様におこなって、
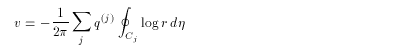(2.10)
これらをまとめると、
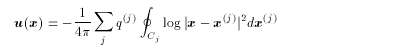(2.11)
となる。つまり、コンターの位置 { x ( j )
} がすべてわかれば、
この式より任意の点の速度が求められる。
コンター上での速度も求められるので、それでコンターを移流させることにより、
コンターの時間発展を求めることができる。