2.4 流体塊の変形に関する有限時間リアプノフ解析
Yoden and Nomura(1993)
は、 相空間内で有限時間リアプノフ解析をおこなった。 ここでは、同じ解析を実空間でおこない、流体塊の変形の線形的な指標を導く。流体粒子の軌跡は、
(2.16)
の解軌道 x ( t ) で与えられる。
これからの微小な摂動を y ( t )
とすると、 その時間発展は式(2.16)を局所的に線形化した方程式で記述できる。
(2.17)
ここで、J は u の x ( t )
におけるヤコビアン行列である。
式(2.17)を t0 から t0
+τ まで積分した結果は、 行列 M (レゾルベント)を用いて
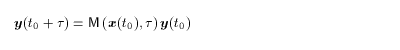(2.18)
とあらわすことができる。
いま、ある初期時刻 t0 において x
( t0 )
のまわりに微小な半径εの円領域を考える。
(2.19)
式(2.18)より、
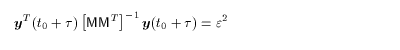(2.20)
となり、円が楕円に変形される(図1)。 その主軸長と主軸方向は、
半正値対称行列 M MT
の固有値・固有ベクトルにより与えられる。
一方、MT M の固有値を e2λi(
x (t0), τ)、 固有ベクトルを fi
( x ( t0 ), τ) とすると、
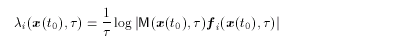(2.21)
である。式(2.18)より、 λi ( x ( t0
), τ) が有限時間リアプノフ指数であり、 fi
( x ( t0 ), τ)
が対応するベクトルである。 τ→∞
の極限をとれば、一般のリアプノフ指数、ベクトルと一致する。
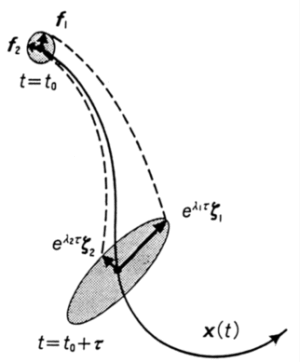図1:
流体塊の変形に関する有限時間リアプノフ解析。
円で囲んだ領域が、有限時間τ後には楕円に変形される。
その主軸長は eλiτ で与えられる。