相変化を起こす 鉛直運動の向き

地球大気の雲において水蒸気の凝結は上昇運動に伴って生じている。 しかしこれは実は自明なことではない。

飽和条件の決まり方

凝結が生じるには、凝結成分の分圧が飽和蒸気圧に達する必要がある。 そのためには、

• 圧力を高めることにより凝結成分の分圧を稼ぐ
• 温度を下げることにより飽和蒸気圧を下げる

のどちらかを生じさせねばならない。

鉛直対流問題においては、この二つは競合関係にある。 たとえば流体が断熱的に上昇する場合には：

• 圧力が低下し、凝結成分の分圧も低下する。これは相変化に不利である。
• 断熱膨張によってパーセルの温度が低下し、飽和蒸気圧が下がる。これは相変化に有利である。

の二つが競合する。このうちのどちらが勝つかによって、 凝結が上昇に伴って生じるか下降に伴って生じるかが定まる。

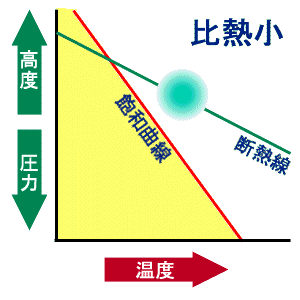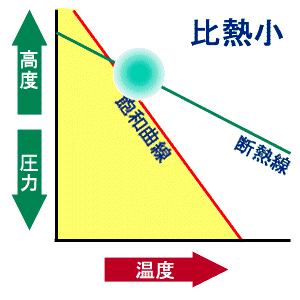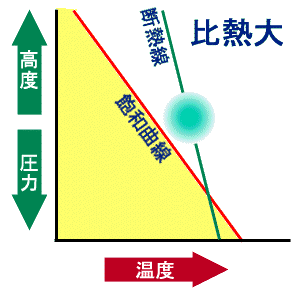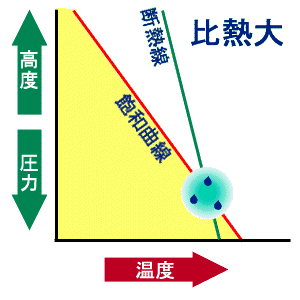
図1:主成分比熱の違いよる凝結条件の違い。 定量的計算はこちら。

この問題は McDonald(1964) が定量的に議論している。その結果 (詳細は付録を参照。) 要点は以下に整理できる。すなわち：

• 飽和蒸気圧の温度依存性は凝結成分の潜熱に依存
• 断熱膨張に伴う温度変化は主成分の定圧比熱に依存

という事情があるので、凝結が上昇・下降のどちらで生じるかは凝結成分の潜熱と主成分の定圧比熱に 依存し、凝結は

• L ＞ L^c  または c_pn ＜ c_pn^c のとき上昇流
• L ＜ L^c  または c_pn ＞ c_pn^c のとき下降流

で起こる。ただし、 L^c＝ c_pnR_vT/R_n、 c_pn^c＝ LR_n/R_vT である。
[なお、R_n  は主成分の気体定数； R_v は凝結成分の気体定数； c_pn は主成分の定圧比熱；L は凝結成分の凝結の潜熱(いずれも 単位質量あたり)； T は温度である。]
凝結成分の蒸気圧曲線(従って L )を固定し、c_pn を変えた場合の凝結条件の違いを図１に示す。

なお、上を変形すると凝結条件は、主成分のモル定圧比熱 C_pn = c_pnR/R_n および凝結成分のモル凝結エントロピー S^cond = LR/TR_v [ R は普遍気体定数]を用いて、 S^cond ＞ C_pn なら上昇流で凝結、S^cond ＜ C_pn なら下降流 で凝結と書ける。

実際の地球惑星対流では？

表１：代表的凝結物質のモル凝結エントロピー。

物質	温度(K)	Scond(J/mol K)
H2O	270	168
NH3	250	92
CH4	100	86

実際の惑星大気中の代表的な凝結成分について、もっともらしい温度での モル凝結エントロピーは表１の様になっている。 ( McDonald(1964)の数値には誤りがある。)

純物質のモル比熱は単原子分子で 5/2 R = 21、二原子分子で 7/2 R = 29 程度なので、主成分のモル定圧比熱は 20〜30 (J/mol K) 程度と考えられる。 表１のモル凝結エントロピーはこれよりずっと大きい。従って 地球の水蒸気雲を含め全てにおいて凝結は上昇流で生じることがわかる。

以上は下降運動に伴う相変化は形而上学的なものであると示唆しているかにみえる。 しかし、これはあくまで対流する流体が気体であると考えたからである。 もし作業流体が液体であれば、 圧力変化に伴う体積変化が小さく、断熱膨張・圧縮に伴う温度変化も小さいため、飽和蒸気圧の温度依存性の効果は相対的に重要でなくなり、 圧力変化による分圧変化の効果が勝つ ことになり、相変化(この場合は固化)は下降運動に伴って生じるであろう。 実際、地球中心核の液体部分(外核)においては下降運動 で鉄の固化が生じていると考えられている。

相変化を起こす鉛直運動の向き