脚注

マントル対流など

マントル対流は粘性が極めて大きく従ってその温度依存性などの影響が顕著であるので、相変化を導入する以前に対流の様相は複雑になる(たとえば鳥海ら(1997)を参照)。
またマントル・地殻中で生じるマグマ生成は、極めて粘性が大きい固相の中で相対的に粘性の小さい液相・気相が生じ重力分離(この場合は上昇)を起こすという点において、雲対流に多少似ている(たとえば小河(1997)を参照)。

[本文に戻る]

McDonald(1964)の数値の誤り

McDonald(1964) に示されているモル凝結エントロピーの値は、一部不適切であるようだ。そのため、例えばメタンが下降流で凝結する可能性など、誤った議論が含まれている。なお、本論文に記した値は、The National Institute of Standards and Technology (NIST) の Chemistry WebBook に掲載されている飽和蒸気圧曲線から Clausius Clapeyron の関係を用いて計算した。

[本文に戻る]

定量的に計算した飽和条件

主成分比熱の違いよる凝結条件の違いを、凝結物が水蒸気である場合について定量的に計算した。
縦軸：飽和蒸気圧および凝結物の分圧。
横軸：温度。
黒：飽和蒸気圧曲線。
赤：C_pn = 3.5 R
緑：C_pn = 35 R
の場合。(温度285Kでの分圧を 1000Pa とした。)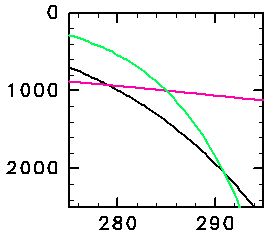

[本文に戻る]

周囲が飽和していない場合

周囲が飽和していない場合には、考えているパーセルと周囲との凝結成分の混合比の差はさらに大きくなる。これによる浮力の増減は、分子量比(＝凝結物の分子量／主成分の分子量)による。すなわち：

分子量比＞１→負の浮力が増す
分子量比＜１→正の浮力が増す

である。

[本文に戻る]

凝結物が浮力に与える効果

凝結物は周囲の流体に対してほぼ終端速度で落下する。この状態では凝結物に働く重力は流体圧によって支えられているので、結局、パーセルは下向きに引きずられる。この引きずり力によって、分子量比などにかかわらず、正味の浮力は減少する。したがって、浮力生成のための条件はさらに厳しくなる。

[本文に戻る]

パーセルと周囲の温度差が有限である場合

簡単のために分子量比が１より十分大きいとする。このとき、凝結物質による負の浮力は、q に(q は凝結物質の質量混合比)比例するが、周囲の温度がパーセルの温度より q T₀ ( T₀ は基本場の温度)以上低ければ、分子量効果は完全に打ち消される。

[本文に戻る]

下降流での凝結？

計算結果を見ると最下層に凝結物があるのみであり、これでは下降流での凝結が起こっているか疑わしく感じられるかもしれない。しかし、最下層が凝結している状態が定常的に維持されていることを考えると、対流運動に伴って上方から下降してくるパーセルが、最下層に差しかかるとともに順次凝結しつつある状態であることが了解されるであろう。

[本文に戻る]

熱対流というより組成対流

結果の図から、温度偏差と水蒸気混合比に負の相関がみられる。これは最下層での凝結の結果であり、ほぼ

c_p T' = - L q

の関係にある。この関係から、温度偏差と水蒸気混合比による浮力の比は：

(T'/T₀ )/ q = -L/(c_pT₀ )

となる。数値を代入すると、この実験では -0.024 であり、水蒸気混合比による浮力が圧倒的に大きい。

[本文に戻る]

地球中心核の熱的境界条件

本研究では地球中心核の対流においても相変化は流体の中で生じるとして扱い、その下にある固体核の影響は無視した。しかし、室内実験で熔融合金などを下から冷やして固化させる際に生じる組成対流では、相変化は、流体内部ではなくその下にある固体の結晶成長としておこることが知られている [Huppert,1990; Tait and Jaupart,1992; Neilson and Incropera,1991]。またダイナモを導入した地球中心核対流の数値モデリング [Glatzmaier and Roberts, 1996]でも固体核表面の境界条件について、これを想定した設定がなされている。これらの論文における想定と本研究における想定のどちらが現実的かは、冷却の強度・対流の速度・結晶成長の速度など多くのパラメタに依存するであろうと思われ、研究が必要である。

[本文に戻る]

脚注