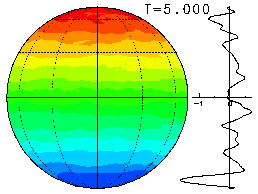3.1 渦度場および帯状流の時間発展の概観
 実空間での流れ場の時間発展を渦度場と帯状流の変化をとおして概観する.
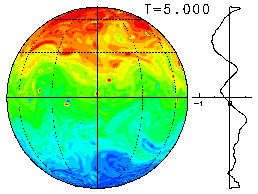
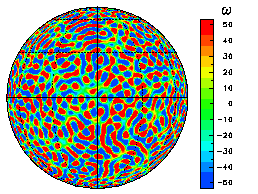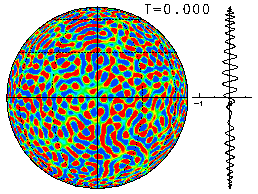
ランダムに与えた初期値(の一例)を渦度ωの場として表示すると右図のようになる.
実空間での流れ場の時間発展を渦度場と帯状流の変化をとおして概観する.
ランダムに与えた初期値(の一例)を渦度ωの場として表示すると右図のようになる.
初期値パラメターは, n0=50, γ=1000, で, 切断波数 T341 である.
ここで, 赤色が正の渦度, 青色が負の渦度である.
また, 渦度場の右側には帯状平均した帯状角運動量(u cosφ)の分布を示す.
渦度場の表示は, 赤道上空からの正射図法で, 経線・緯線は30度毎に描いている.
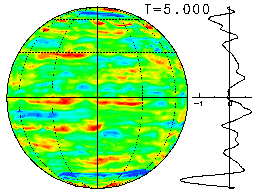
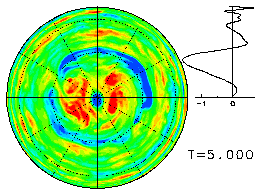
3種類のΩ(=0, 50, 400)について, この同一の初期値から出発した時間発展 を以下に示す. 下図は, それぞれ各Ωに対する最終状態を描いているが, マウスでクリックすると, 初期値からのアニメーション表示が見られるように なっている.
なお, Ω≠0の場合については, 近似的トレーサーである絶対渦度
q = ω + 2Ωμ の場を表示しているため, 南北で惑星渦度(2Ωμ)分の
ゲタが含まれていることに注意が必要である.