|
B. モデルの離散化 |



| |
離散化の概要を以下に示す.
- 空間差分
- 基礎方程式は直交 Lorenz 型スタッガード格子上の有限差分によって離散化する.
スカラー量(温位, ダスト混合比, 乱流エネルギー)の移流と連続の式は 4
次中央差分で離散化する. 運動量の移流と圧力の空間微分, 乱流拡散項,
ダストの重力沈降は 2 次中央差分で離散化する.
中央差分に伴う格子サイズの数値的ノイズを消去するために,
乱流エネルギーとダスト混合比に対してはラプラシアンの 3
乗に比例する人工粘性を, 運動量については速度の空間勾配の 2
乗に比例する人工粘性を加えている.
放射伝達方程式, 地面熱伝導方程式の離散化も 2 次中央差分で行う. CO2
赤外放射フラックスを計算する際の鉛直積分は台形公式を用いて行う.
- 時間差分
- 運動方程式, 熱力学の式, 乱流エネルギーの式,
ダスト移流の式中の移流項と浮力項については leap frog スキームを用いる.
だたし数値解の安定性のため, 10 ステップに 1 回前進差分を用いる.
放射加熱項と乱流拡散項に対しては全ての時間で前進差分を用いる.
ダストの放射伝達方程式は行列の反復計算で解く. 反復回数は 4 回とした.
地中の熱伝導方程式の時間差分は Crank-Nicolson 法を用いた.
以下の各節中において記号の下付き添字 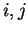 はそれぞれ水平および鉛直方向
の格子点値, 上付き添字 はそれぞれ水平および鉛直方向
の格子点値, 上付き添字 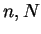 は時間方向の格子点値を表す. 大気中の鉛直格
子点数は は時間方向の格子点値を表す. 大気中の鉛直格
子点数は 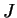 とする. スカラー量と基本場量の空間格子点を整数値にとり,
それから半格子ずれた点を半整数値で表す. 空間格子間隔は水平方向は とする. スカラー量と基本場量の空間格子点を整数値にとり,
それから半格子ずれた点を半整数値で表す. 空間格子間隔は水平方向は 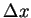 , 鉛直方向は , 鉛直方向は 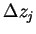 , 時間刻みは , 時間刻みは 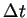 と表す. と表す.
|
2次元非弾性系を用いた火星大気放射対流の数値計算
Odaka, Nakajima, Ishiwatari, Hayashi,
Nagare Multimedia 2001
|



|
|