ロスビー波による解釈 -(3) エネルギー収支

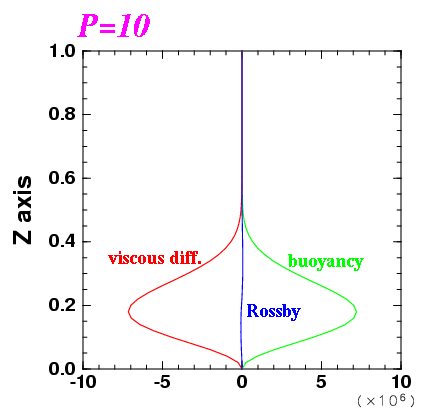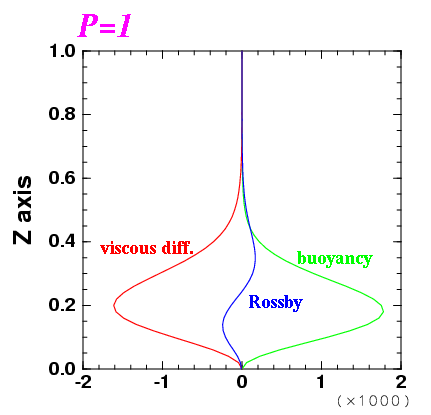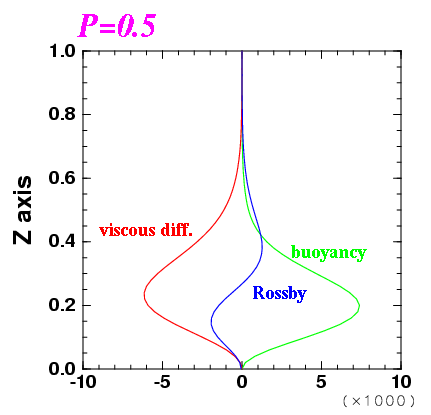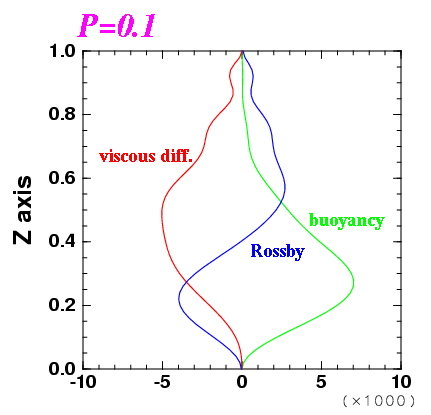
図: 1 波長平均した運動エネルギー収支. 緑線が浮力による運動エネルギーの生成, 青線がロスビー波による運動エネルギー輸送の発散収束, 赤線が粘性による運動エネルギーの散逸である.

ロスビー波がどこで励起され, 伝播し, 散逸しているかを確かめるべく, 臨界状態付近の対流構造に対して運動エネルギー収支を計算した.

線形化した渦度方程式に $\psi$ をかけて x 方向に平均をとると次のような式が得られる (詳細は付録:運動エネルギーの式).

$\begin{displaymath} \DP{}{t}\left(\frac{1}{2}\overline{\vert\Dgrad\psi\vert^2}\... ...R\overline{\theta\DP{\psi}{x}} -P\overline{(\Dlapla\psi)^2}. \end{displaymath}$

(10)

ここで上線は x 方向の 1 波長平均を表している. 左辺第 1 項が運動エネルギーの時間変化, 第 2 項がロスビー波の伝播に伴う運動エネルギーの収束, 第 3 項は粘性による運動エネルギー輸送の収束である. 右辺第 1 項は浮力による運動エネルギーの生成, 第 2 項が粘性による運動エネルギーの散逸に対応している.

臨界状態付近の対流構造に対してこの式の各項の強さの z 分布を描いたのが上図である. 臨界状態に近いので運動エネルギーの時間変化項は無視できる. 右辺第 3 項の粘性による運動エネルギー輸送の収束は実際に計算してみると粘性散逸に比較して十分に小さいので描いていない.

プランドル数が小さい場合
ロスビー波によるエネルギー輸送が十分に大きい. 下で発散, 上で収束 → 上向きにエネルギー輸送
浮力によるエネルギー生成は領域下側に集中.
粘性散逸は領域上側までのびている.
プランドル数が大きい場合
ロスビー波によるエネルギー輸送が非常に小さい.
浮力によるエネルギー生成と粘性散逸が領域下側でほぼバランスしている.

このことから, 運動が引き起こされている様子が以下のようにはっきりとわかる.

プランドル数が小さい場合
下側で運動が引き起こされる → ロスビー波として上方へ伝播 → 粘性で散逸.
プランドル数が大きい場合
下側で運動が引き起こされる → その場で粘性散逸.