| 有限振幅計算 |
|
|
|
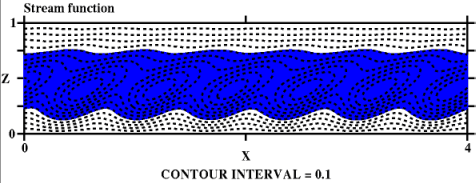
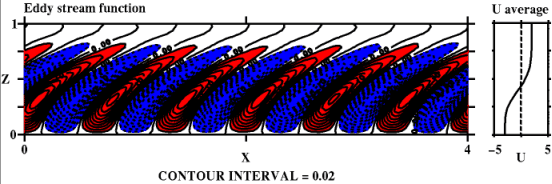
| 図: 有限振幅対流の計算結果. P=0.1, E=10-4, R=1.3x105. 上段が流線関数, 下段が流線のx方向平均からのずれと平均流. |
|
|
|
上図はレイリー数を臨界値よりも大きくした場合に 発生する対流の構造を時間積分により計算したものである (計算方法の詳細は付録:有限振幅計算詳細). 流線関数を示した上図では等値線が横に伸びており, 強い x 方向の平均流が引き起こされていることがわかる. そのことをはっきりと示すために x 平均とそれからのずれで 表現したのが下図である. 上側領域で x 正方向(東向き), 下側領域で x 負方向の平均流が存在している. 擾乱流線関数の図には線形計算に見られたようならせん状の構造が見られる.
この平均流の生成は傾いた対流セルによる運動量輸送により説明することが多い.
すなわち, 速度の x および z 成分
u, w の相関によって生じるレイノルズストレス
しかしながらこの平均流生成も次のようにロスビー波の性質を通して理解することができる.
|