３．実験結果及び考察

 
３．６　不安定波の同定
 

R =350のf 軸を通過する波束の時間変化を示している。 f 方向の空間分解能は動画3および図6の等値線分布図の5倍となっている。 黒線で囲まれた乱流塊の通過前と後では、それぞれ青と赤の矢印で示すように異なる種類の不安定波が現れることが明確にわかる。どちらも進行しているのでその波面は時間軸に対して傾く。 青矢印で示した不安定波は赤矢印で示した不安定波に比べ周期(1/f )が短く、それぞれ無次元周波数  =f /wD で 22〜29,  3.8〜4.5である。 これらはItoh(1998b)の線形安定理論が予測するS-CおよびC-F進行波の周波数と非常に近い(付録2)。 また、時間軸に対する波面の傾きから、どちらの不安定波もf 方向において吹き出し孔から離れるほど位相が遅れている。これを考慮すると、図6に示される各不安定波のf 軸に対する波面の傾きは符号が異なるから、それぞれの不安定波はR 方向には互いに逆方向に伝播することがわかる。Itoh(1998b)の理論結果もS-C不安定波はR 方向外側に、C-F不安定波はR 方向内側に向かって伝播することを示しており、このことは二つの不安定波を識別する上で重要な性質の違いである。 以上の結果から、局所乱流塊は伝播方向の異なる二つの不安定波、すなわちS-C不安定とC-F不安定に起因する進行波を伴うことがわかった。ただし、乱れの強い領域は二つの不安定波の中間に位置し、どちらの不安定波が乱流遷移に寄与しているのか不明確である。S-C不安定は臨界レイノルズ数がC-F不安定に比べて低いものの、増幅率がC-F不安定よりも小さい(Itoh 1998a,b)ため、乱流遷移に直接寄与するのはC-F不安定であり、S-C不安定の寄与は少ないと考えられてきた。しかし、図7を見るとS-C不安定波の波面の延長線上に乱れの強い領域があり、S-C不安定波も乱れの発生に寄与している可能性は十分考えられる。

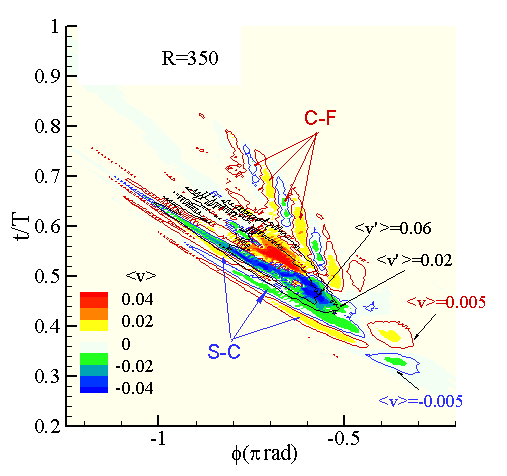
図7　f -t 断面における速度変動の集合平均値<v >の等値線分布.　図中赤線及び青線で囲われた領域はそれぞれ<v >≧0.005, <v > ≦-0.005となる領域を示す.  黒線は乱れ強さの集合平均値.