|
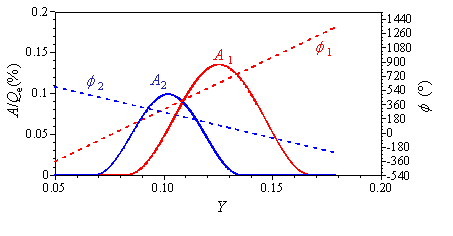
同じ周波数をもつ2つの波動は,それぞれの位相速度が異なり振幅分布が空間的に変化する場合には,線形的な重ね合わせによっても激しい振幅変調を生じさせる可能性があることが,簡単な代数式からわかっている7).各Y位置におけるMode1とMode2の振幅と位相がそれぞれA1(Y),
A2(Y),φ1(Y),φ2(Y)と表される正弦波とすると,重ね合わされた波動
A*(Y)sin[2πft-φ*(Y)]=A1(Y)sin[2πft-φ1(Y)]+
A2(Y)sin[2πft-φ2(Y)], ・・・・・(2)
の振幅と位相はそれぞれ
A*(Y)=
A12+A22+
2A1A2cos(φ2-
φ1),
・・・・・(3)
φ*(Y)=
φ1+ tan-1[A2sin(φ2-
φ1)/{A1+A2cos(φ2-φ1)}],
・・・・・(4)
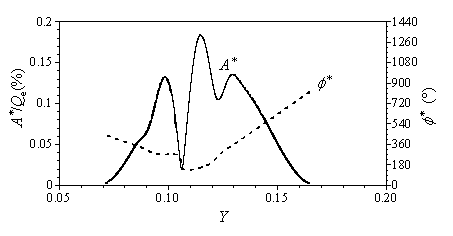
と表せる.注目すべき点は,合成された振幅A*が2つの波の位相差(φ2-φ1)に対して周期的に変化している点である.今考えている流れ場ではφ1とφ2は符号が異なるため,位相差の効果は元の分布の約1/2という短い波長で現れると予測される.またA1とA2がともに同程度の大きさである場合,変調の影響は強く現れる.
図8aに示すような適当な振幅および位相分布を与えると,計測された振幅分布(図6b)とほとんど一致する振幅分布(図8b)が得られることが確かめられる.
|