Next: 4.4 帯状流を維持するフィードバックが無い場合 Up: 4.3 順圧平均流の線形安定性解析 Previous: 4.3 順圧平均流の線形安定性解析
基本流
![]() は、
は、![]() 方向の波数
方向の波数![]() の擾乱に対して安定であることが証明できる(Appendixに示す)。よって
の擾乱に対して安定であることが証明できる(Appendixに示す)。よって![]() の擾乱に対しては不安定になり得る。
の擾乱に対しては不安定になり得る。
発達率が最大の順圧固有モードを解析的に考える。![]() ,
,![]() ,
,![]() とし、(7)の基本場を用いる。
古川 & 新野(2006)[4]の図7より、
とし、(7)の基本場を用いる。
古川 & 新野(2006)[4]の図7より、![]() のときの発達率最大のモードでは
のときの発達率最大のモードでは
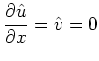 |
(18) |
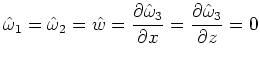 |
(19) |
| (20) |
| (22) |
| (23) |
この結果は、![]() ,
,![]() ,
,![]() ,
,![]() として行った線形安定性解析でも得られた。図16(左)は固有モードの
として行った線形安定性解析でも得られた。図16(左)は固有モードの![]() の構造である。これは古川 & 新野(2006)[4]の図7とも一致している。
の構造である。これは古川 & 新野(2006)[4]の図7とも一致している。
このように、![]() かつ
かつ![]() というのは非常に特殊な状況である。ここで求めた
というのは非常に特殊な状況である。ここで求めた![]() の順圧固有モードは非粘性の場合には非特異中立モードになるものである。したがって、非粘性の場合には
の順圧固有モードは非粘性の場合には非特異中立モードになるものである。したがって、非粘性の場合には![]() の不安定モードが存在する(例えば、新野(1981)[5]を参照)。今考えている系には粘性があるが、
の不安定モードが存在する(例えば、新野(1981)[5]を参照)。今考えている系には粘性があるが、![]() が1よりある程度小さい場合には実際に不安定モードが存在する。図16(右)は
が1よりある程度小さい場合には実際に不安定モードが存在する。図16(右)は![]() で線形安定性解析を行った結果である。このとき発達率は正となり、擾乱の波長を僅かに大きくするだけで順圧不安定が生じることが分かった。
で線形安定性解析を行った結果である。このとき発達率は正となり、擾乱の波長を僅かに大きくするだけで順圧不安定が生じることが分かった。
時間発展では、ロール状対流の発達によって初期のsin型水平シアが歪み、不安定な順圧固有モードが現れた。このように、初期のsin型水平シア流が僅かに歪むだけで順圧不安定が生じ得ると考えられる。そこで、次式のように僅かにシアが歪んだ基本場について線形安定性解析を行った。
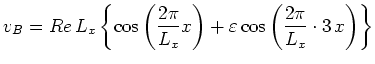 |
(24) |
その結果、![]() の正負に関らず、発達率が正の順圧固有モードが得られた。このことから、シアが僅かに歪んだだけで順圧不安定が生じ得ることが分かる。図18は
の正負に関らず、発達率が正の順圧固有モードが得られた。このことから、シアが僅かに歪んだだけで順圧不安定が生じ得ることが分かる。図18は![]() ,
,![]() のときの
のときの![]() の分布である3。特に、
の分布である3。特に、![]() のときの分布は、古川 & 新野(2006)[4]の図5,d)によく似ている。
のときの分布は、古川 & 新野(2006)[4]の図5,d)によく似ている。
以上より、![]() という設定が、初期のsin型順圧シアについては順圧不安定は起こり得ないが、僅かに順圧シアが歪むだけで順圧不安定が生じ得るという特殊な状況を与えていることに注意したい。
という設定が、初期のsin型順圧シアについては順圧不安定は起こり得ないが、僅かに順圧シアが歪むだけで順圧不安定が生じ得るという特殊な状況を与えていることに注意したい。
SAITO Naoaki