式(4),(8)の各変数を基本場( )と摂動(
)と摂動(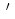 )に分け、両式を線形化すると次の摂動方程式が得られる。
)に分け、両式を線形化すると次の摂動方程式が得られる。
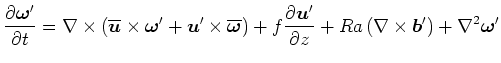 |
(10) |
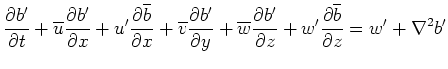 |
(11) |
ただし、基本場は定常かつ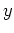 方向に一様なので、基本場成分の時間微分・
方向に一様なので、基本場成分の時間微分・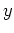 微分は0となる。
微分は0となる。
次に、摂動が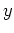 方向に周期的であると仮定すると以下のように書ける。
方向に周期的であると仮定すると以下のように書ける。
ただし、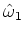 ,
,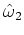 ,
,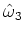 ,
,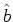 ,
,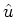 ,
,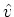 ,
,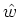 ,
,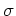 は全て複素数とする。
は全て複素数とする。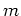 は
は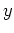 方向の波数、
方向の波数、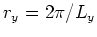 である。
である。
以下の関係式を用いると、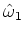 ,
,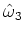 から
から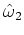 ,
,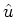 ,
,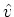 ,
,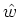 が求まるので、
が求まるので、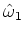 ,
,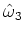 ,
,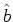 の3つを独立な変数とする。
の3つを独立な変数とする。
以上より、式(10)の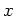 ,
,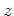 成分と式(11)を計算すると次のようになる。
成分と式(11)を計算すると次のようになる。
式(15)〜(17)に対して固有値解析を行う。計算方法の詳細はAppendixで述べる。
SAITO Naoaki
2008-03-07
![]() 方向に周期的であると仮定すると以下のように書ける。
方向に周期的であると仮定すると以下のように書ける。