4.4 帯状流を維持するフィードバックが無い場合

古川 & 新野(2006)[4]では帯状流を維持するフィードバックが無いため、sin型シア流は定常解ではなく減衰して行く。以下に、3.2節の帯状流を維持するフィードバックが無い場合の計算の解析結果を示す。

• 運動エネルギーの時間変化を見ると(図19)、粘性の影響により順圧平均流成分が(時刻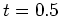$t=0.5$頃を除いて)常に減少し続けている。ロール状対流が形成される時刻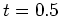$t=0.5$頃に順圧平均流成分・傾圧成分が増加する。ロールが壊れ始める時刻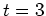$t=3$以降、順圧渦成分が僅かながら増加する。


• 図20は、順圧渦成分の各波数の運動エネルギーの時間変化を示したものである。帯状流を維持するフィードバックがある場合には、まず波数4,5成分が発達した後それらの相互作用により波数1成分が急激に発達したが、帯状流を維持するフィードバックが無い場合では、波数6,4,5の順に発達した後に波数1が発達している。


• 順圧渦成分へのエネルギー変換を示した図21より、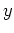$y$方向に波数6の擾乱が現れる時刻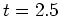$t=2.5$以降に傾圧成分からの大きな変換が見られる。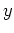$y$方向に波数1の擾乱が現れる時刻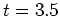$t=3.5$頃には順圧平均流成分からの変換も見られるが、傾圧成分からの変換に比べて相対的に小さい。


• 順圧渦成分への変換について、帯状流を維持するフィードバックがある場合の図6とない場合の図21を比較する。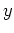$y$方向に波数4〜6の擾乱が発達し始める頃に見られる傾圧成分からの変換の大きさは帯状流を維持するフィードバックがある場合とない場合でほぼ等しいが、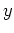$y$方向に波数1の擾乱が現れる頃に見られる順圧平均流成分からの変換は帯状流を維持するフィードバックがない場合の方がある場合に比べて1桁以上小さい。


• これは、帯状流を維持するフィードバックがない場合において粘性の影響によりsin型シアが弱まると、帯状流を維持するフィードバックがある場合に比べて順圧平均流成分の運動エネルギーが減少する一方で、傾圧成分の運動エネルギーは主に上面と下面の温度差(本研究では固定)によって規定され、水平シアの強さの違いの影響を受けにくいためと考えられる。

図19: 順圧平均流・順圧渦・傾圧 各成分の運動エネルギーの時間変化

図20: 順圧成分の各波数(0,1〜6)の運動エネルギーの時間変化 (拡大)

図21: 順圧平均流・傾圧 成分から順圧渦成分へのエネルギー変換の時間変化

• 以上の結果を見ると、帯状流を維持するフィードバックが無い場合は、順圧波数1の擾乱の発達には順圧不安定が効いていないように見える。しかし、順圧波数1成分に限定したエネルギー変換を計算してみると図22のようになり、順圧平均流成分から順圧渦成分への変換のほとんどは順圧波数1成分への変換で占められており、傾圧成分からの変換と同程度の順圧平均流からの変換があることが分かる。よってこの場合においても、順圧波数1成分の発達には順圧不安定が本質的に効いていると考えられる。


• なお、図21に示されている傾圧成分から順圧渦成分への大きなエネルギー変換を波数ごとに分解したものが図23である。これを見ると、その多くは波数6への変換で占められており、これは4.2節で示したのと同様に、ロール状対流の不安定モードである波数6成分(4.2節のフィードバックのある場合では波数4,5であった)が順圧成分を持っており、それが発達することに対応している。


• この計算では、かなり振幅が小さい初期擾乱から出発しているため、ロール状対流が壊れる時刻が古川 & 新野(2006)[4]のものよりも更に遅く、順圧波数1成分が発達する時刻における帯状流の順圧平均流成分が粘性により非常に弱くなっており、そのため順圧波数1成分への変換を見ても(図22)、傾圧成分からの寄与が順圧平均流からの寄与と同じくらいになってしまっている。しかし、古川 & 新野(2006)[4]では、より早いタイミングで順圧波数1が発達しているので、もし彼らが本研究と同様に順圧波数1成分に限定したエネルギー変換を計算していれば、傾圧成分からの寄与よりも順圧平均流からの寄与の方が大きくなっていたはずである。

図22: 順圧平均流・順圧渦(波数2以上)・傾圧 成分から順圧渦成分(波数1)へのエネルギー変換の時間変化

図23: 傾圧成分から順圧渦成分の各波数(1〜6)へのエネルギー変換の時間変化