|
| 2. モデルと実験設定 | [prev] [index] [next] |
使用するモデルは, 球面 3 次元プリミティブ方程式系に基づく 地球流体電脳倶楽部版 AGCM5 である (SWAMP Project, 1998; Hayashi et al., 2000). このモデルはいわゆる簡略な大気大循環モデル(GCM)で, 水輸送と簡単な物理過程を含む.
物理過程には以下のスキームを用いている.
Kuo スキームは, HS86 において使われていた積雲パラメタリゼーションであり, wave-CISK 的構造を作りやすいと想定されているスキームである. 一方, Numaguti and Hayashi (1991)等により, 湿潤対流調節スキームを用いると wave-CISK 的構造は コヒーレントな時空間構造としては生じにくいことが分かっている. 本研究では, この様な対照的性質を示す事が期待される二つの積雲パラメタリゼーションを 用いた数値実験を行い, その結果を対比する. これらの積雲パラメタリゼーションの概要については 付録Dの 簡単な解説を参照されたい.
運動方程式, 連続の式, 熱力学の式, 水輸送の式は, 水平方向にはスペクトル法, 鉛直方向には差分法で離散化されており, 解像度は, 水平波数 T42(全波数1から42を持つすべての球面調和関数を 基底に用いる), 鉛直 16 層である. 鉛直レベルは, 対流圏に12レベル,成層圏に4レベルが置かれているが, 中でも大気再下層の約500m の範囲に3レベルを集中させて混合層の表現に 努めている.
はじめに述べたように, wave-CISK の理論(付録A) によれば熱帯降水活動の様相は凝結加熱の鉛直分布に強く依存することが期待される. そこで本研究では, 積雲パラメタリゼーションの選択に加えて, 凝結加熱の鉛直分布の違い に対して赤道域の降水活動の時空間構造がどのように異なるかを調べる. しかし, 付録Aで議論されている様な理論的モデルとは異なり, 本研究で用いる様な大気大循環モデルにおいては凝結加熱の鉛直分布は 個々の数値実験の中でモデル中の複数の物理的,力学的プロセスの相互作用の結果として定まるものであり, 外から直接に指定することは出来ない. そのかわり, ここでは間接的に凝結加熱の鉛直分布を制御する.
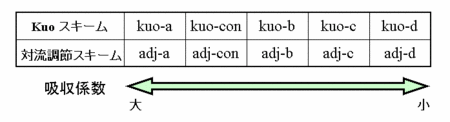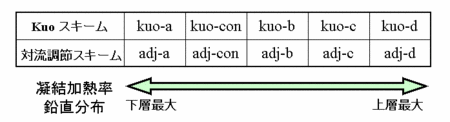
放射冷却の鉛直分布と雲による凝結加熱の鉛直分布は非常に大まかには釣り合うことが知られている (放射対流平衡という; Manabe and Stricker, 1964 ). すると, 鉛直放射冷却率分布を操作することにより凝結加熱率の鉛直分布が間接的に制御できると期待される. そこで, 凝結加熱を間接的に制御する事を目的として, ここでは, それぞれの積雲パラメタリゼーションに対して, 長波放射スキームの乾燥空気の吸収係数に関して, Hayashi et al. (2000) で用いている標準値を中心に, その組み合わせを変更した 5 つのケースの実験を行う (図1.1). 後に見るように, 吸収係数の組み合わせの違いに応じて長波放射の鉛直分布は変化し, これに対応して凝結加熱の鉛直分布も変化する (実験結果: Kuo スキーム図3.1, 湿潤対流調節スキーム図4.1 ). これら10個の実験のうち, kuo-a, adj-a, kuo-c, adj-c の4つを特に重点的に解析する.

|
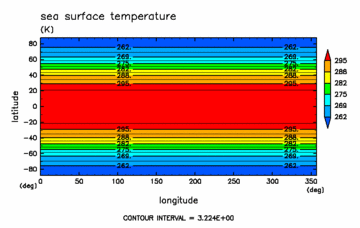
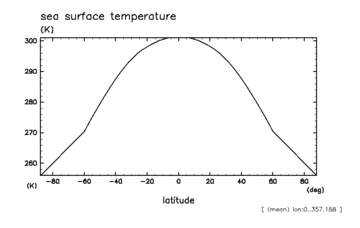
地表面は全て海洋とし海面温度は時間的に一定なものを与える (水惑星条件). 海面温度分布は, Hayashi et al. (2000) で用いられたものと同じ分布を与え る. すなわち, 東西に一様, 南北に対称であり, 緯度 7 度よりも低緯度側で は一定値 302 [K] である (図1.2).
|
|
| 図1.2: 海面温度 (単位は [K]) の水平分布(左) と南北分布(右). | |
|
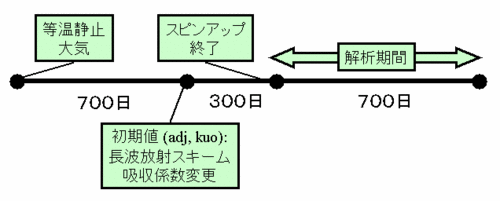
各実験の初期値には, 等温静止大気から実験 kuo-con, adj-con の条件で 700 日間 時間積分したものを用いた. これ以後, 長波放射を変更した後, 300日間の時間積分を行い(スピンアップ期間), その後の700日間のデータを解析する (図1.3). |
|
| [prev] [index] [next] |