| (a) |
|
(b) |

|
| (c) |

|
||
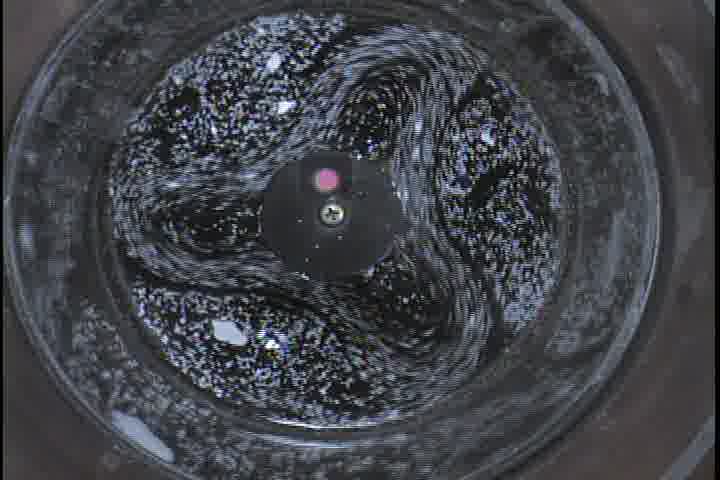
| 図3.1: 高感度カメラで撮影された画像。(a)実験1の結果で実験開始から420秒後、(b)実験2の600秒後、(b)実験3の900秒後。 | |||
| 粒子画像流速測定法と渦運動エネルギーを用いた回転水槽実験で発生する傾圧不安定波の定量化 | << Prev | Index| Next >> |
第3.1節では、回転水槽実験の水面の運動場を粒子画像流速測定法を用いて算出する。その算出した運動場から、流速や相対渦度の分布を示す。第3.2節では渦運動エネルギーによる解析方法を紹介し、その検証を行う。
図3.1は、水槽と同じ速度で回転させて撮影した高感度カメラの各実験結果の画像である。アルミ粉末が白く映っていて、それぞれの実験で発生する水面運動の様子をとらえている。PIV解析を行うことにより、この画像から水面全域の運動を把握することができる。
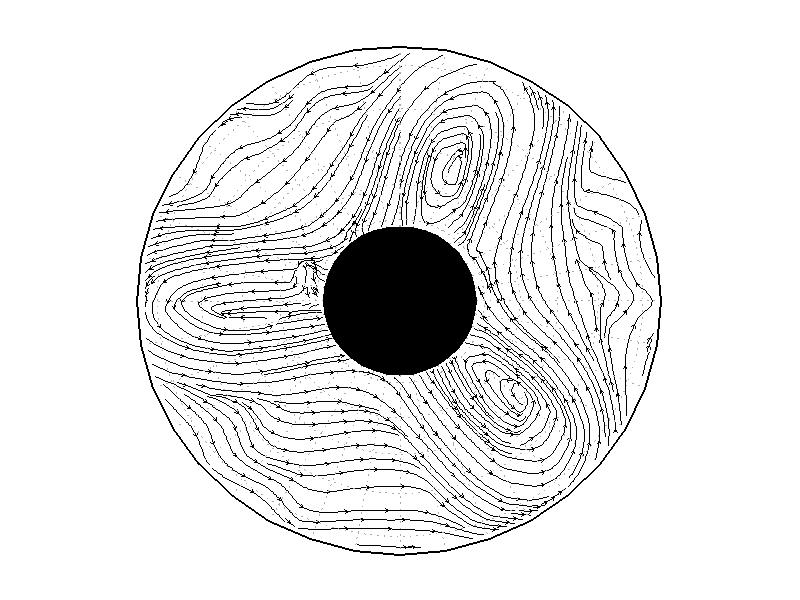
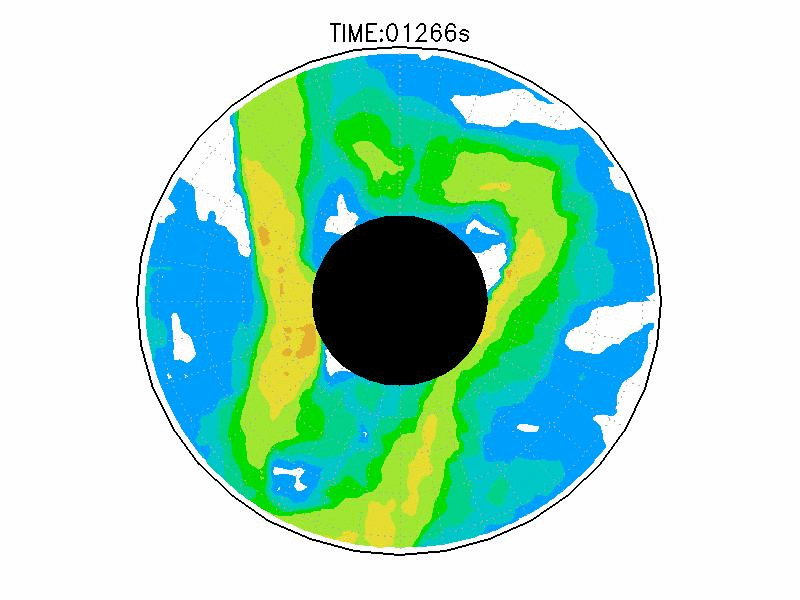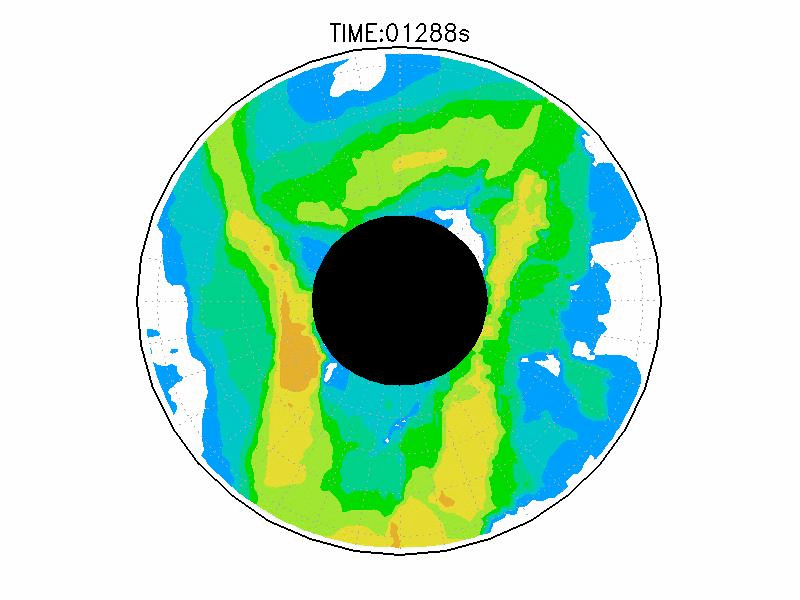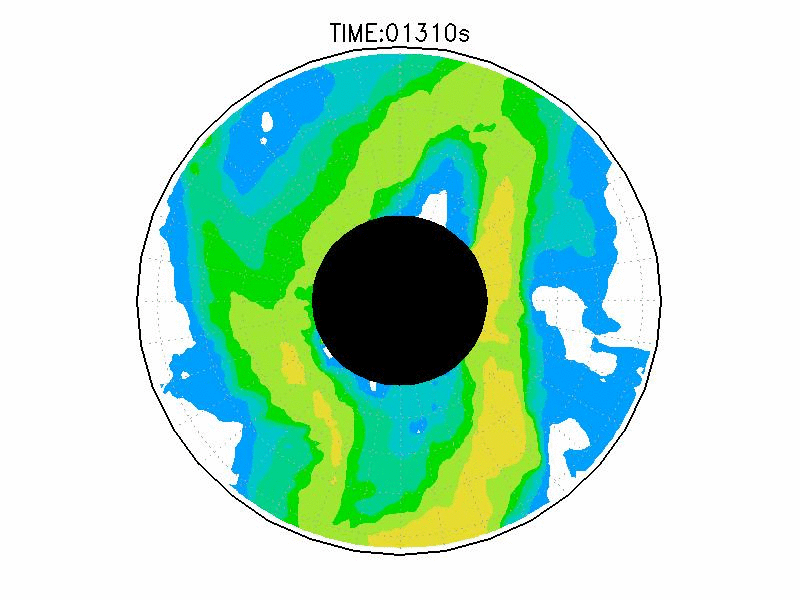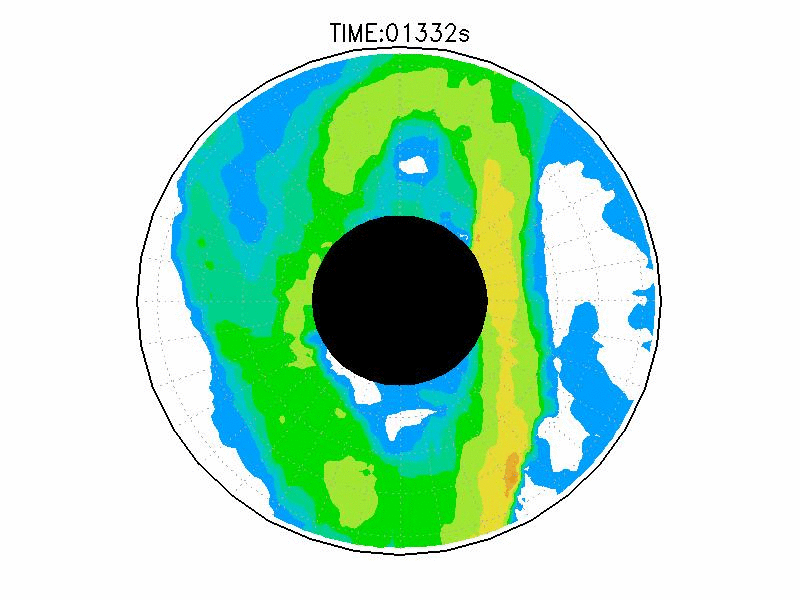
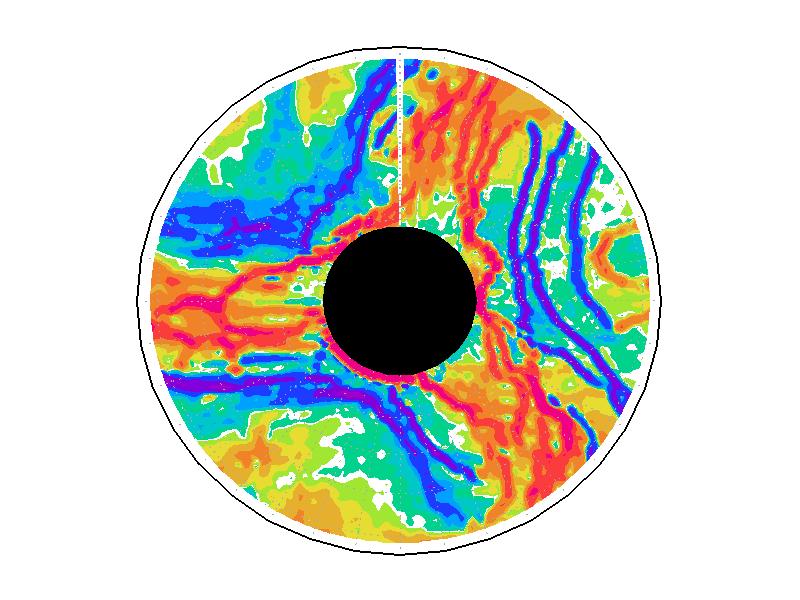
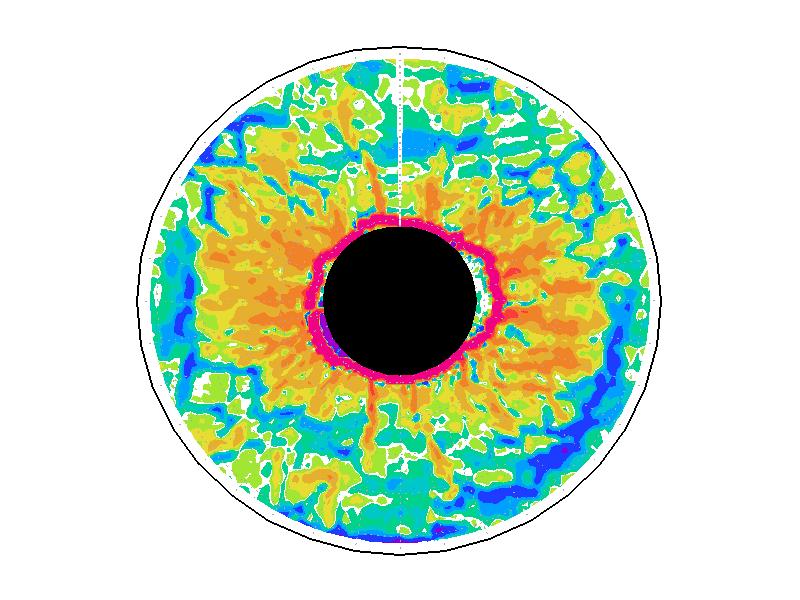
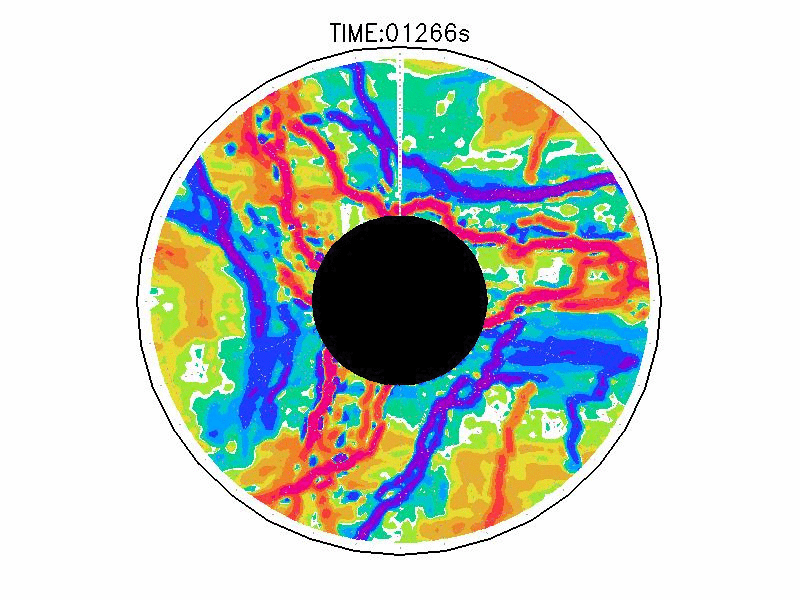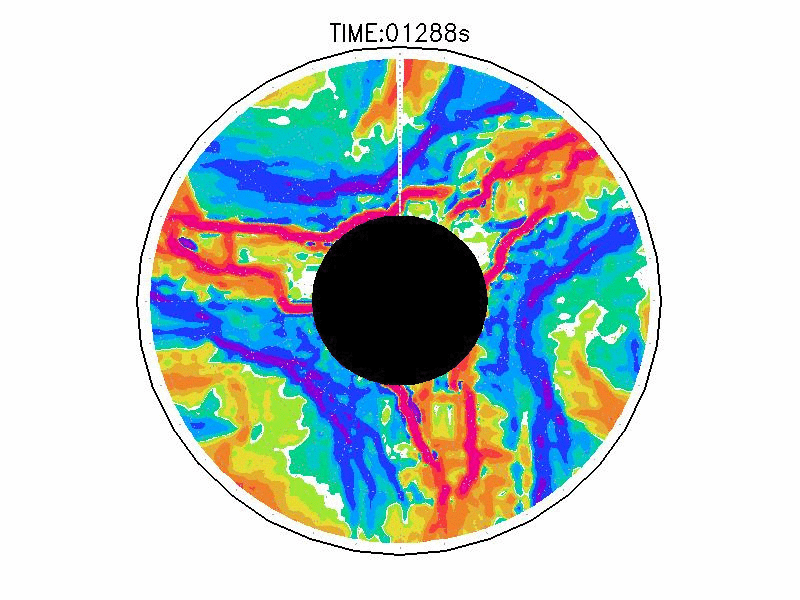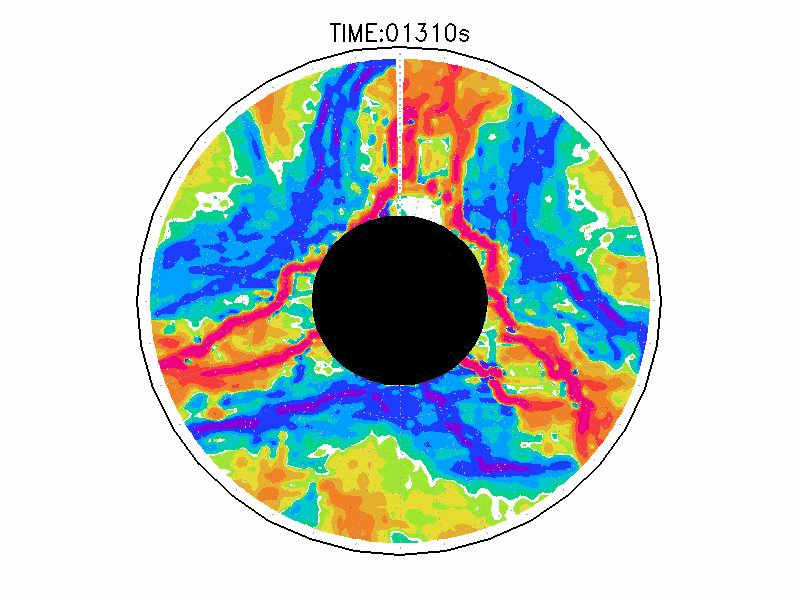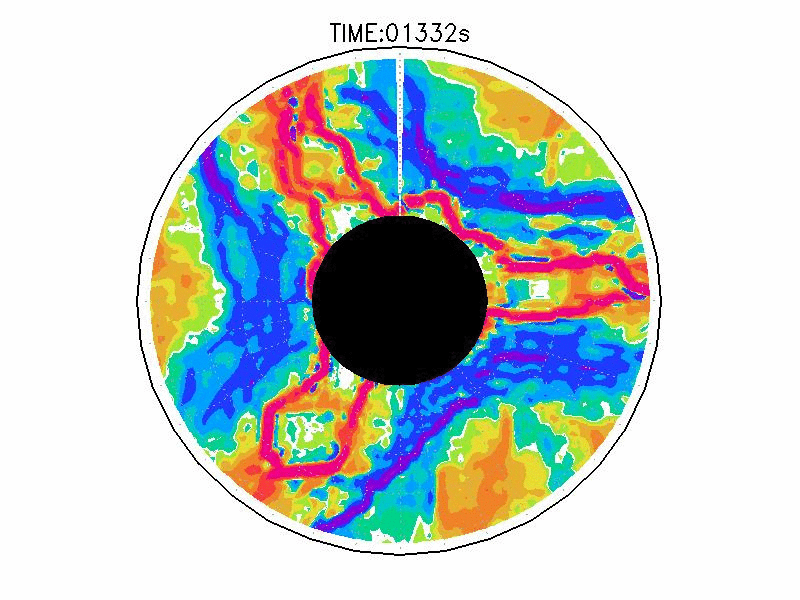
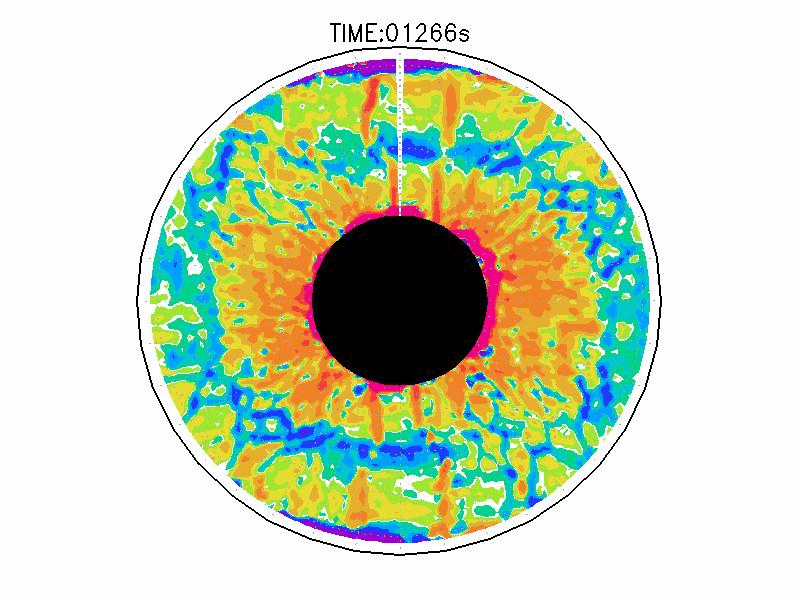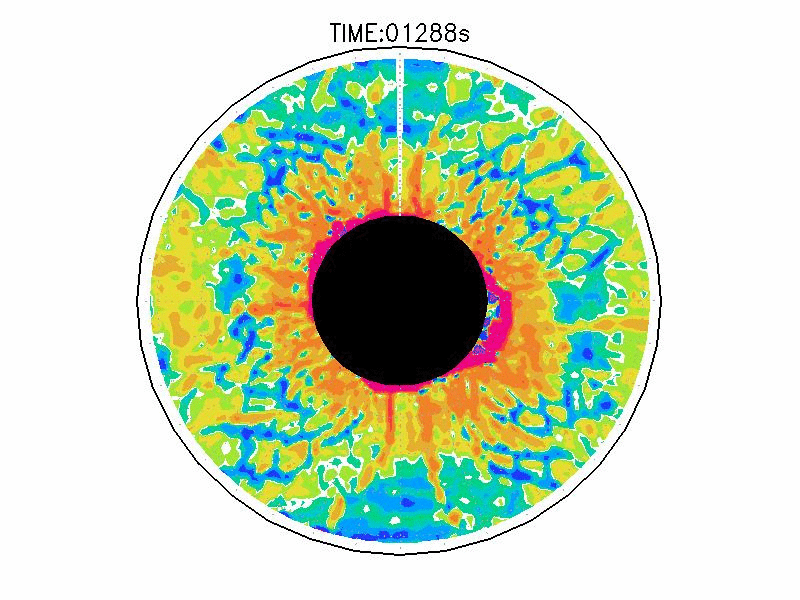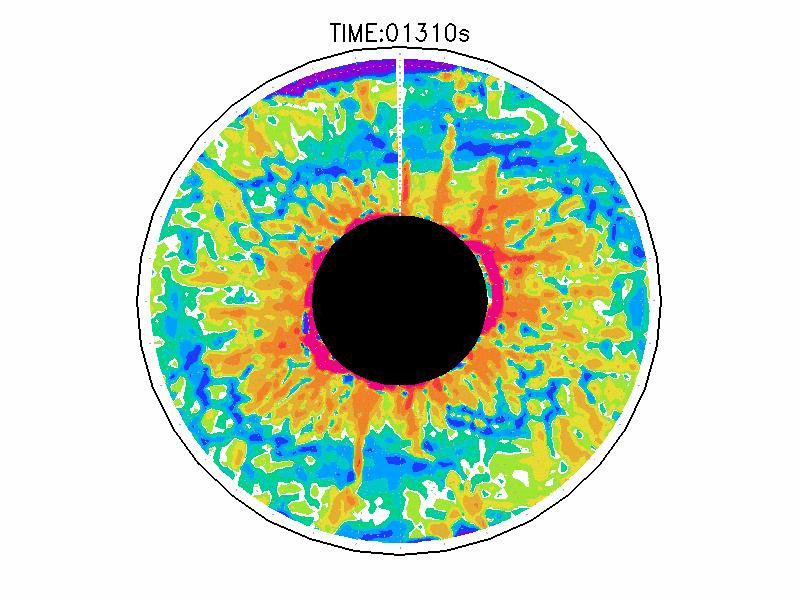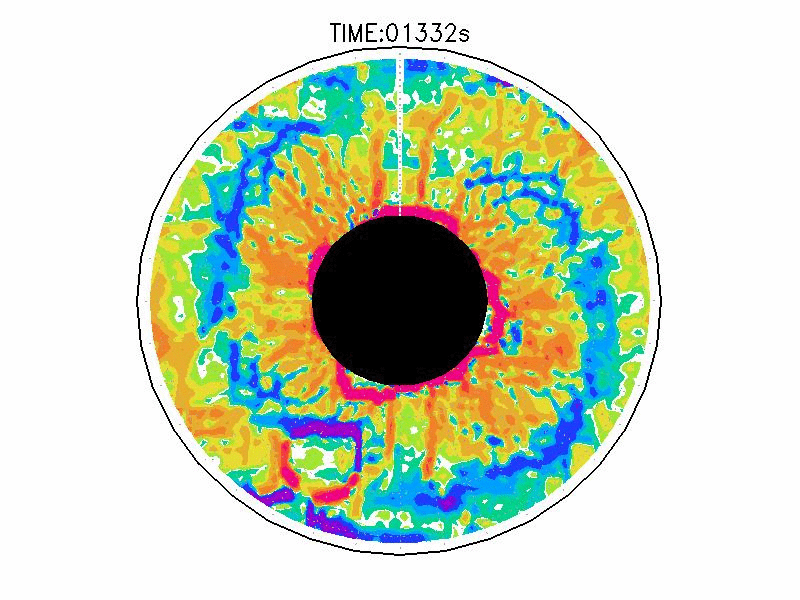
図3.2と図3.3と図3.4は、図3.1の画像から得られた水面の運動ベクトル、速度分布、相対渦度分布である。相対渦度の算出は、PIV解析で得られた格子状の流体運動分布から算出した。実験1の結果では、実験開始からスピンアップ期間を経た420秒後、明瞭な傾圧不安定波が発生している(図3.2aと図3.3a)。本研究では、この1周につながった高速度領域をジェットと呼ぶ。ジェットの速度の大きさは、最大のところでおよそ6.0mms-1であった。ジェットは1周のうち3度の蛇行をしており、この波形や波数は実験期間中でほぼ変わらなかった。相対渦度場でみると、蛇行するジェットの軸の内側で正、外側で負の相対渦度分布となる(図3.4a)。これらの実験期間中の動画を付録3に掲載している。
ここで、温度風関係が成り立っていると考えて、理論値と比較して解析されたジェットの速度を評価する。温度風関係より、流速=(圧力傾度力―遠心力)/ (2x角速度)である。水の密度は理科年表に記載されているもの、求める位置は水槽幅の内側から30mm、水温20℃とした。すると、求まる速度は=0.0046ms-1となる。観測値(6.0mms-1)と比べてやや小さいが、妥当な結果が得られていることがわかった。
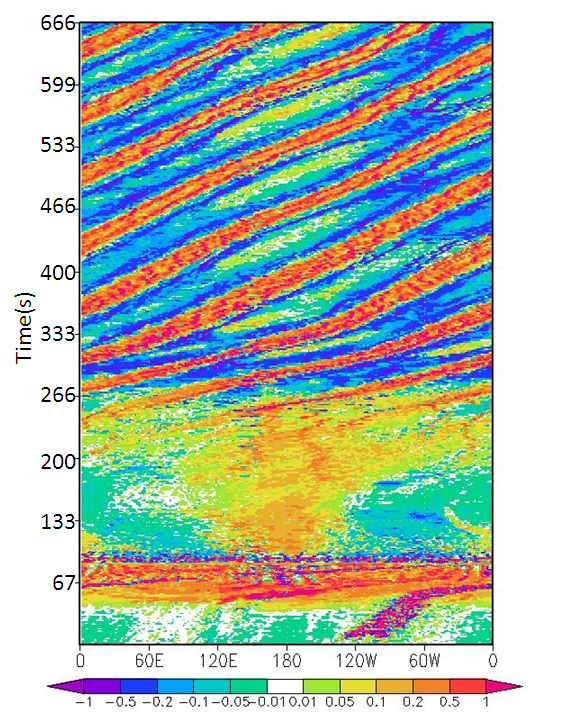
図3.5は、実験槽中央付近(水槽幅の内側から22-44mm)で平均した相対渦度分布の時間変化を示したホフメラー図である。実験開始から約300秒までのスピンアップ期間中はノイズが大きいが、その後、正と負の相対渦度域が規則正しく並んで発生していることが確認できる。ジェットの蛇行に対応した正と負の相対渦度は、水槽の回転方向と同じ反時計回りにまわっている。1周に約200秒を要し、その位相の移動速度は実験期間中ほぼ一定だった。 この半径での円周を考えると、位相の移動速度は1.7mms-1となる。これは、水面流速(平均的に0.5〜4.0mms-1)のおよそ半分の速度であるため、線形論で予測される傾圧不安定波の位相速度と整合的といえる。
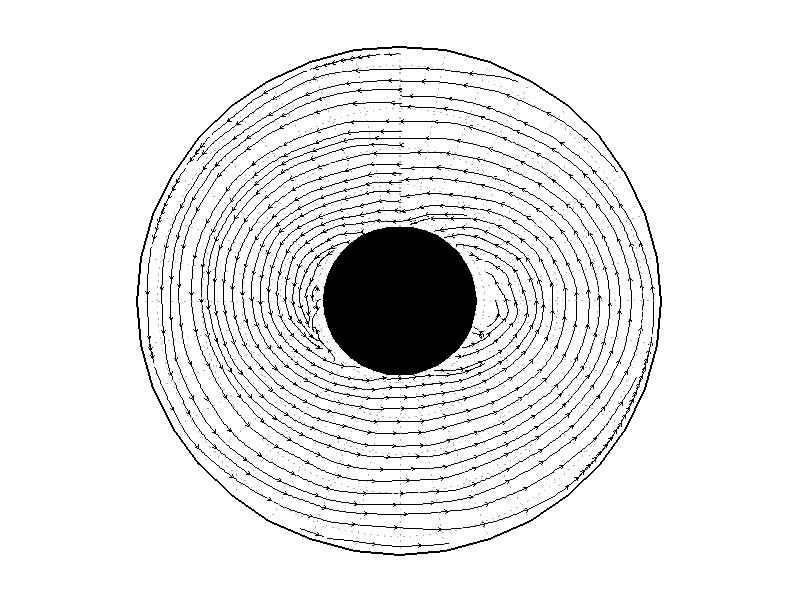
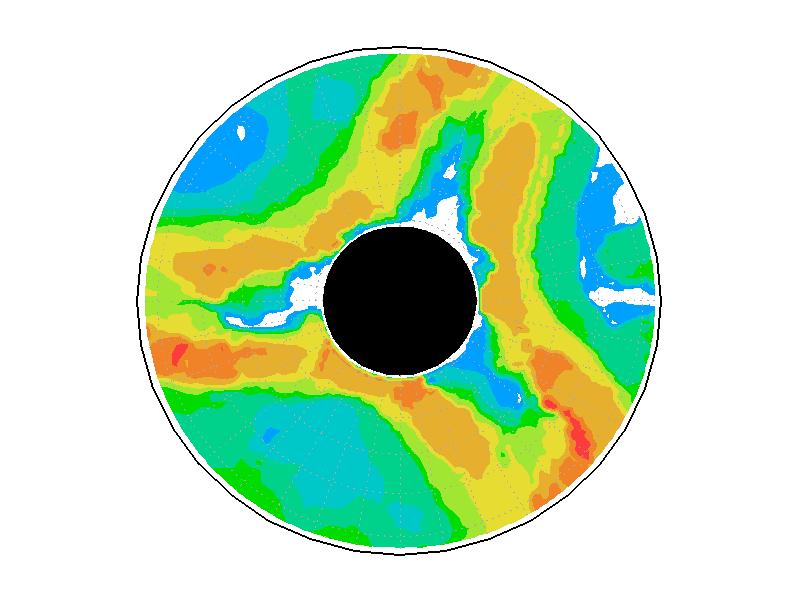
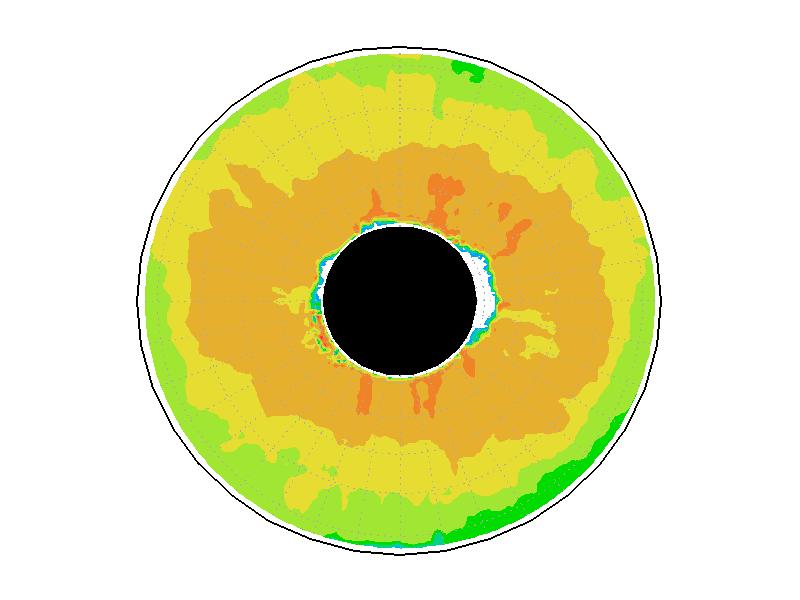
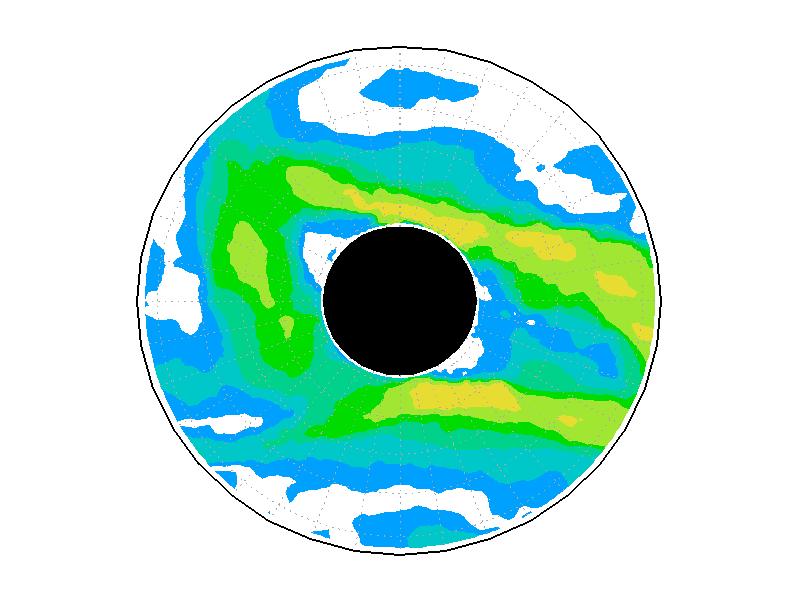
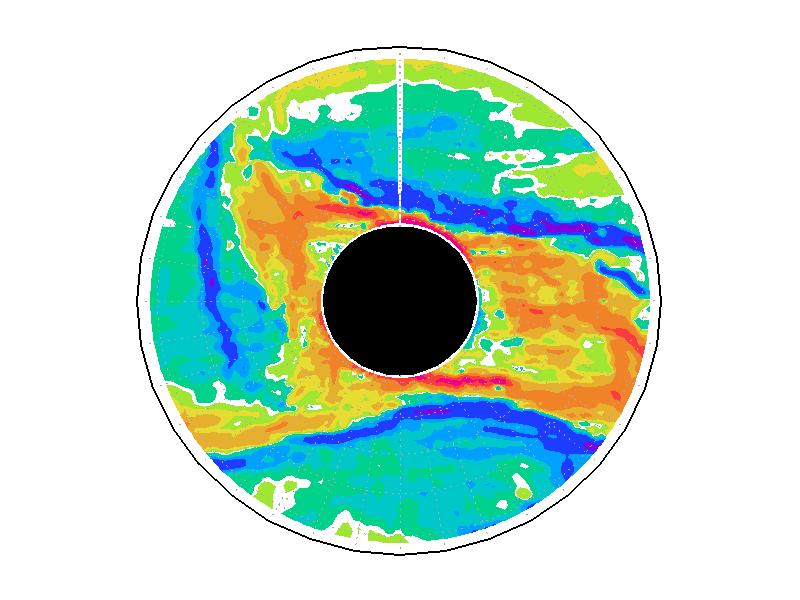
実験2は、円周運動が卓越し(図3.2b)、速度分布は実験槽の中央付近から内側で大きく、ほぼ同心円の分布をしている(図3.3b)。速度の最大は約5.0mms-1である。相対渦度場は、実験1と比べて全域で小さい(図3.4b)。
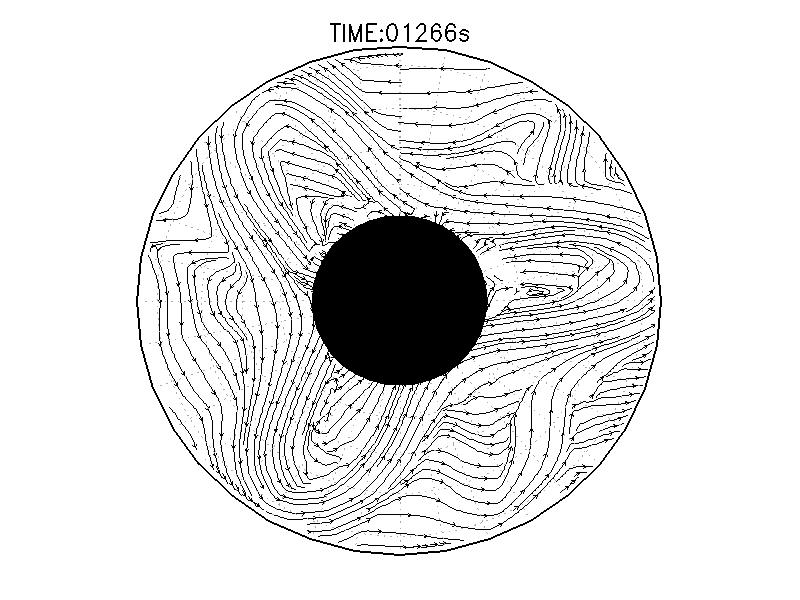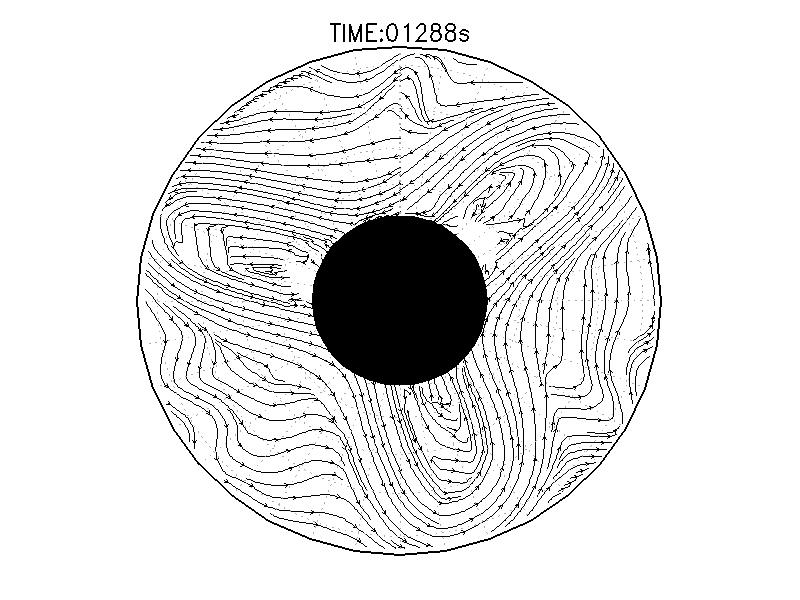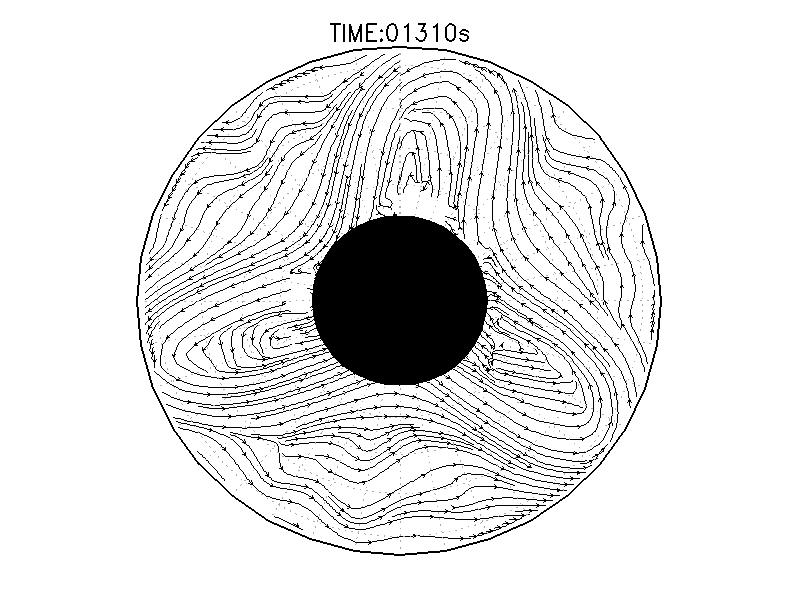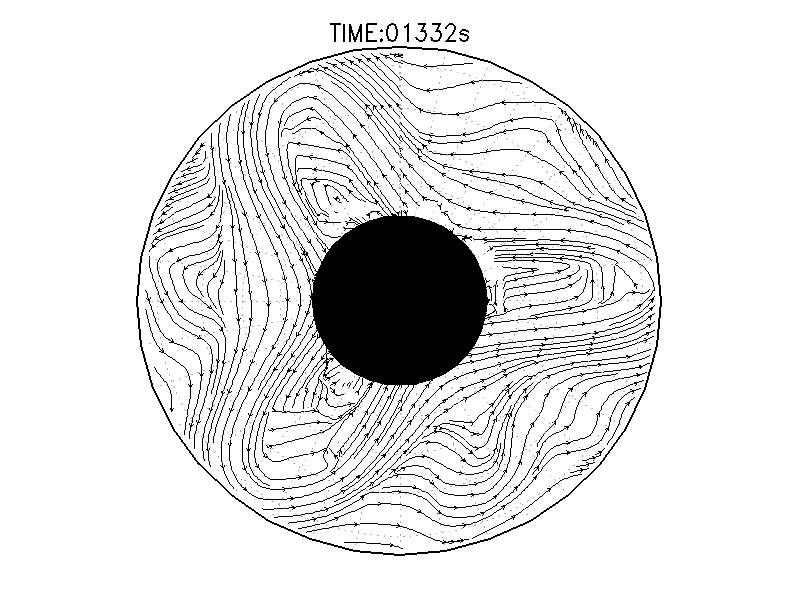
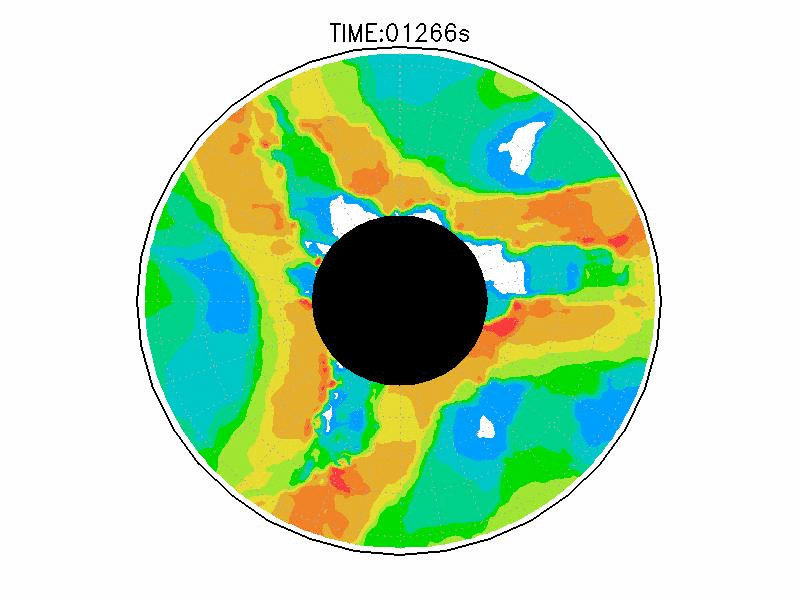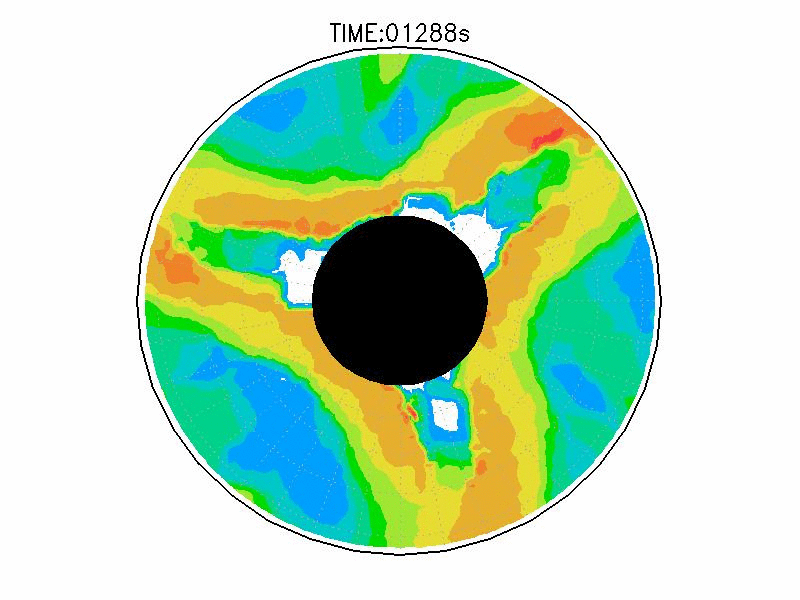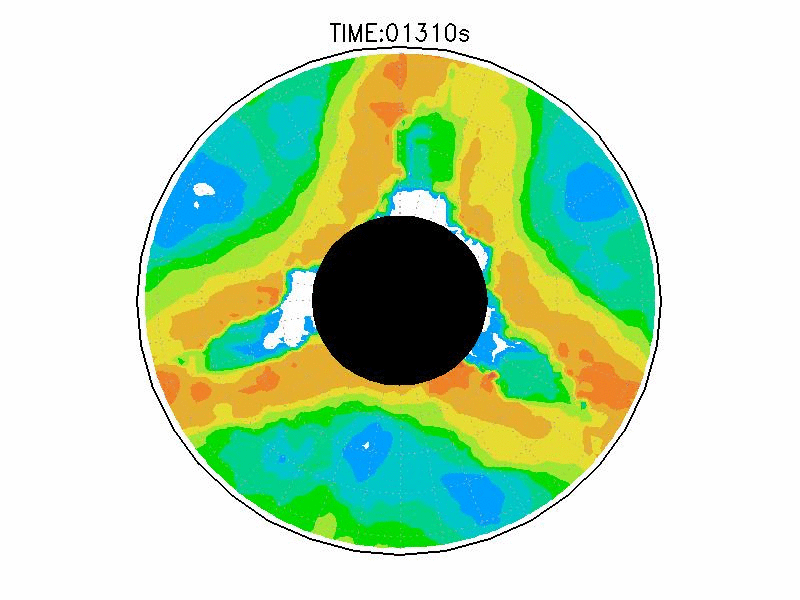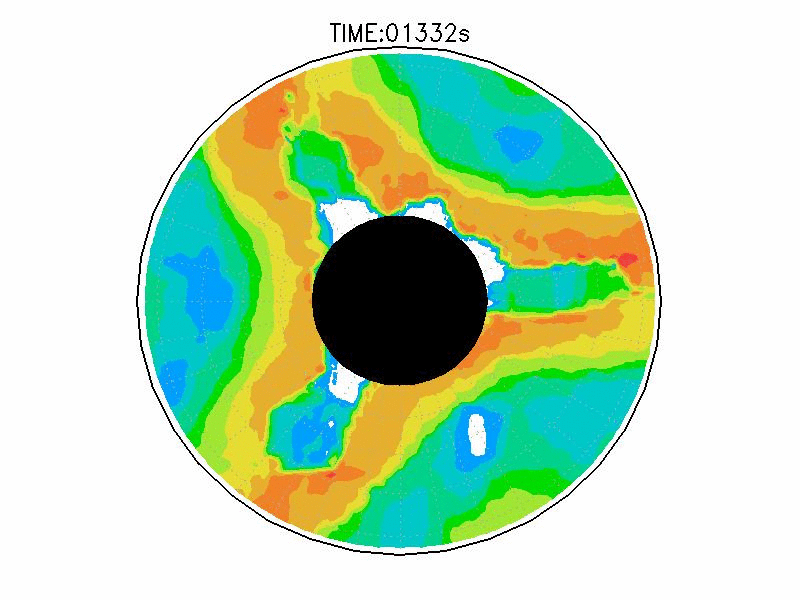
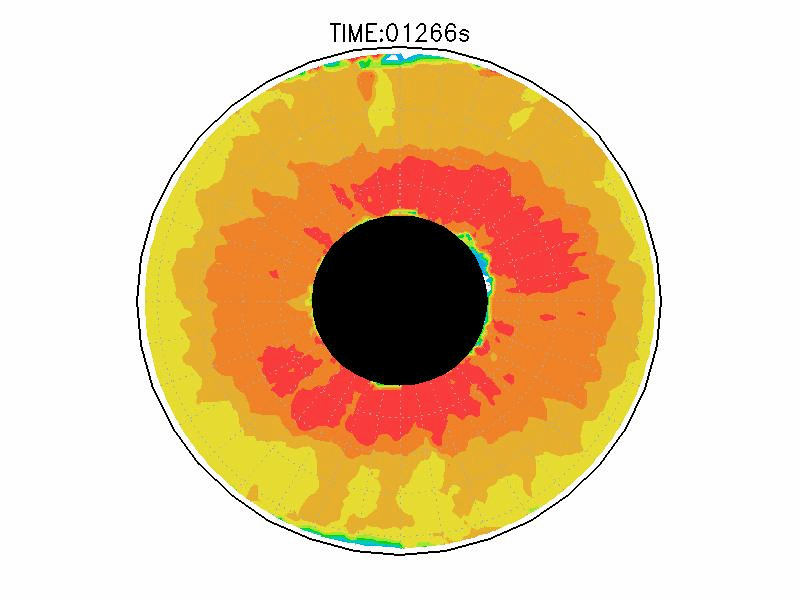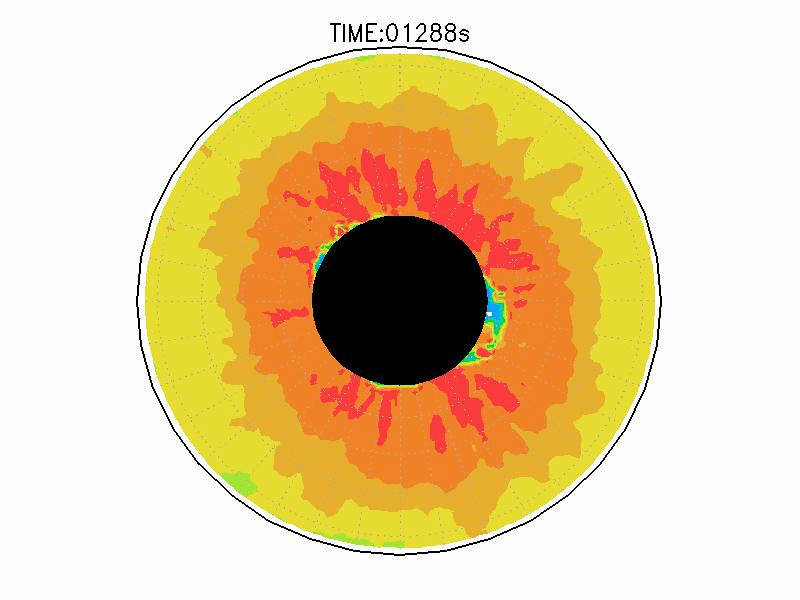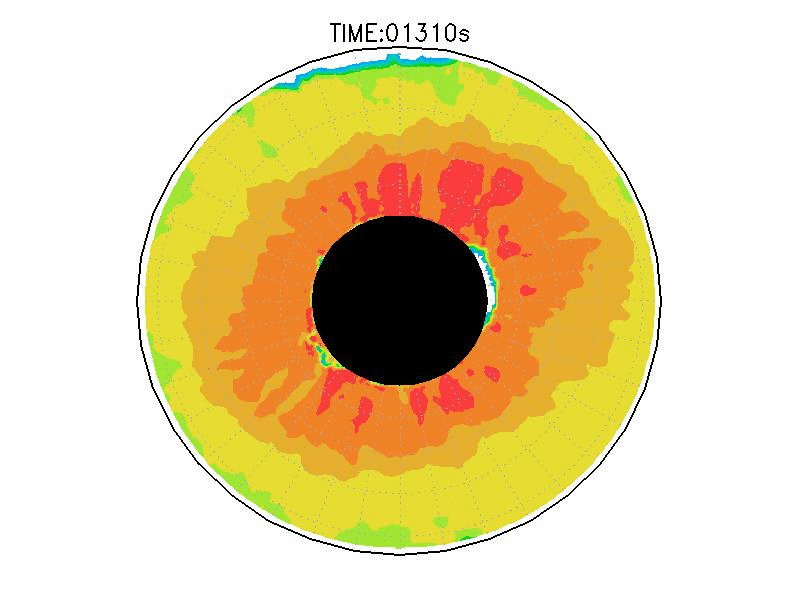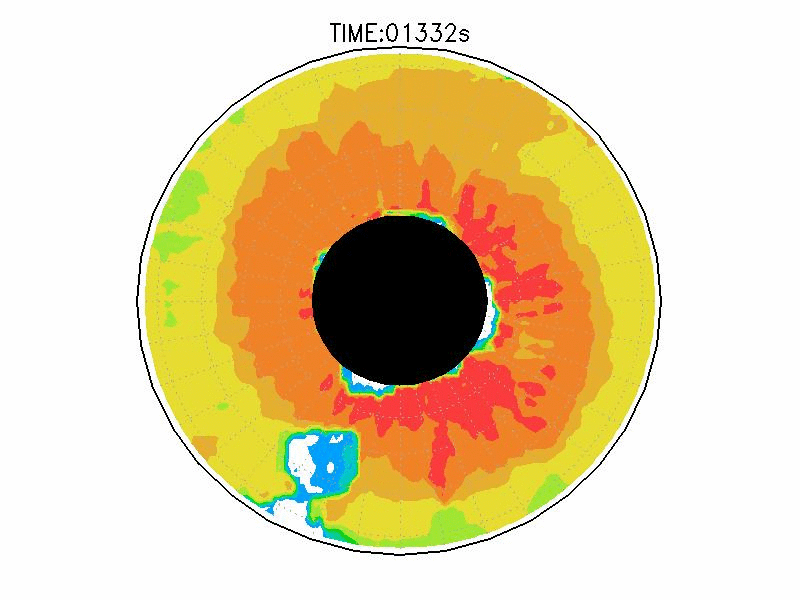
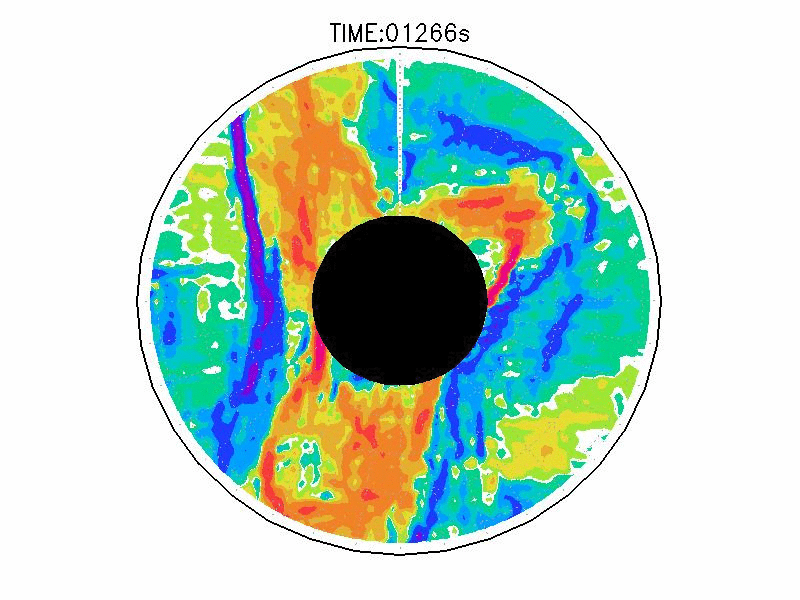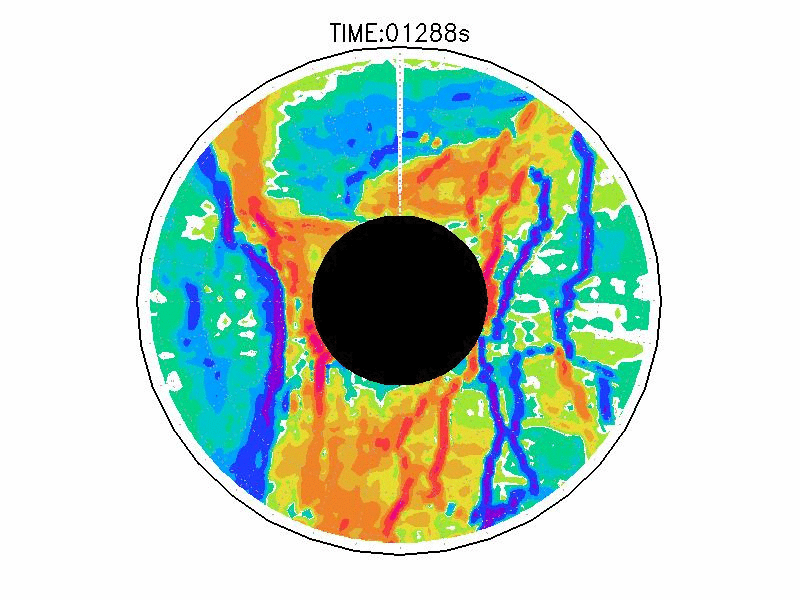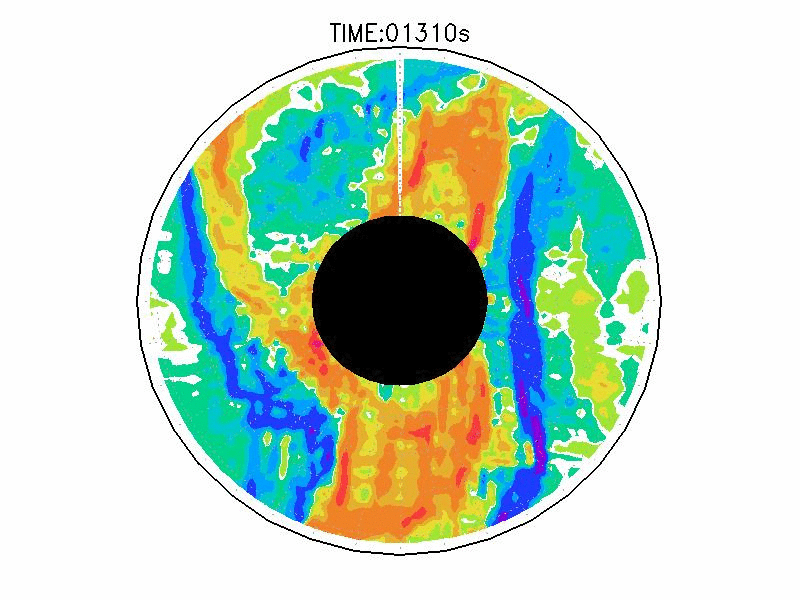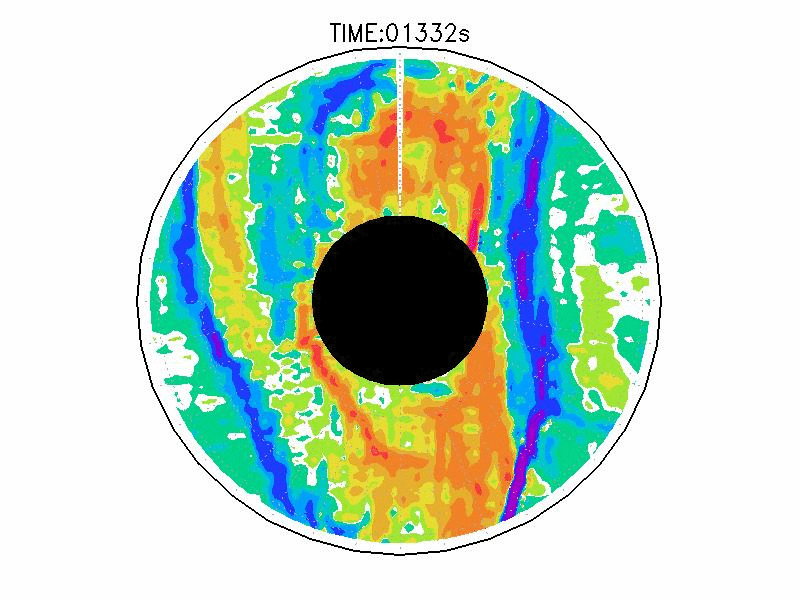
実験3は、波数2とも波数3とも確認できるような、いびつな形に蛇行したジェットが発生している(図3.2cと3.3c)。ジェット軸の速度は約3.0mms-1、相対渦度場はジェット軸の内側で正、外側で負の相対渦度分布となっている(図3.4c)。実験期間中、明瞭な卓越波数を持つようなジェットの蛇行は確認されなかった。
| (a) |

|
(b) |

|
| (c) |

|
||
| 図3.1: 高感度カメラで撮影された画像。(a)実験1の結果で実験開始から420秒後、(b)実験2の600秒後、(b)実験3の900秒後。 | |||
| (a) |
|
(b) |
|
|
|
||
| (c) |
|
||
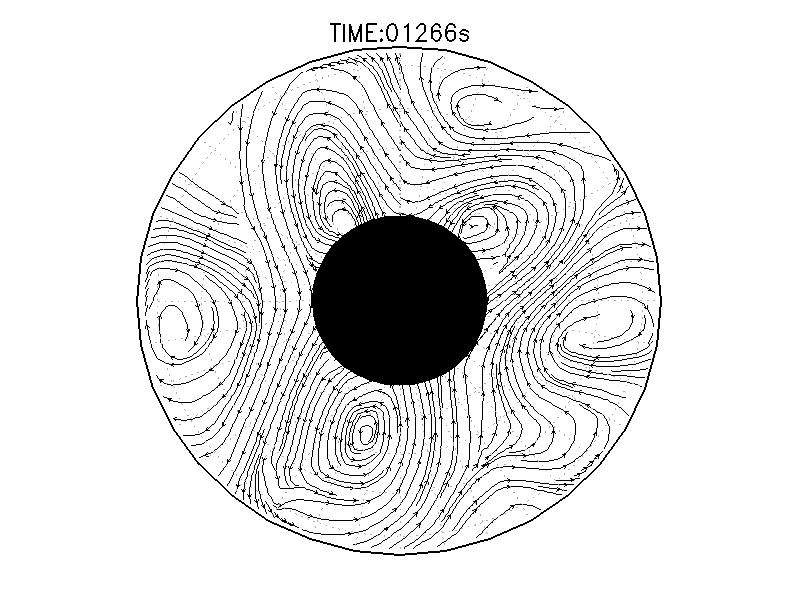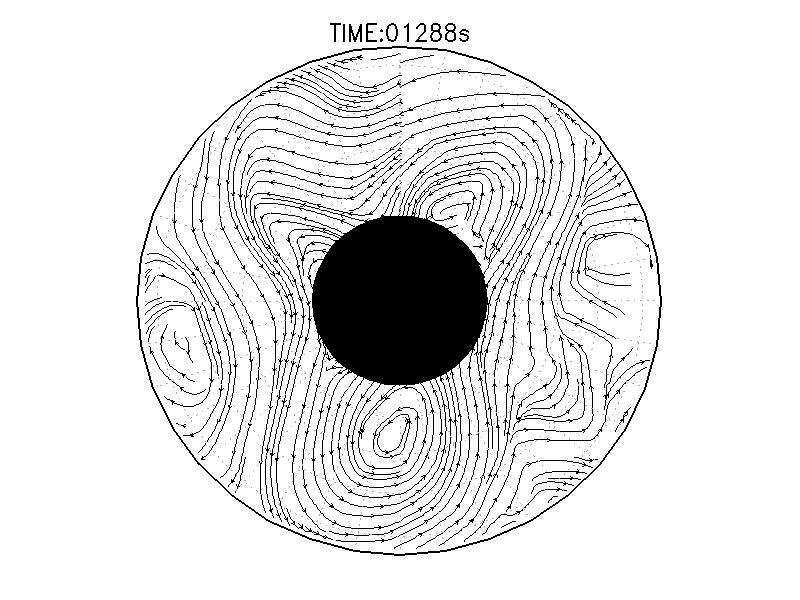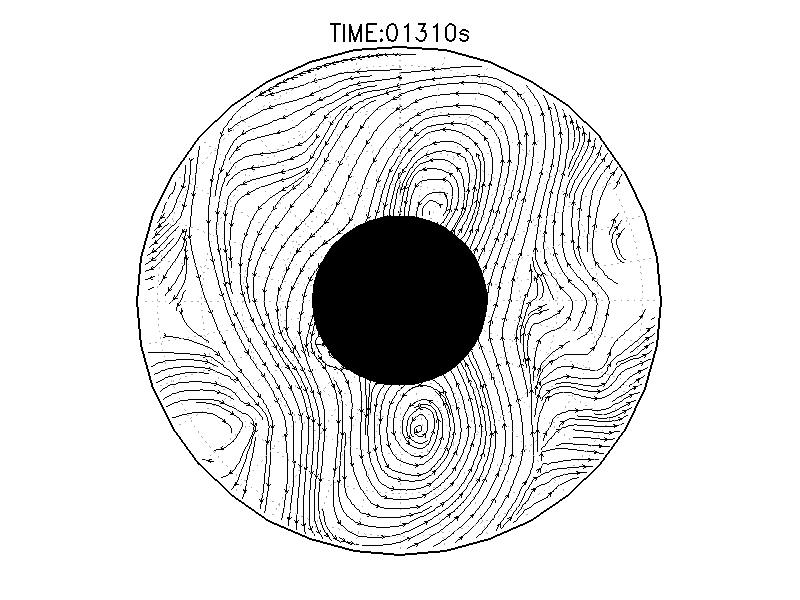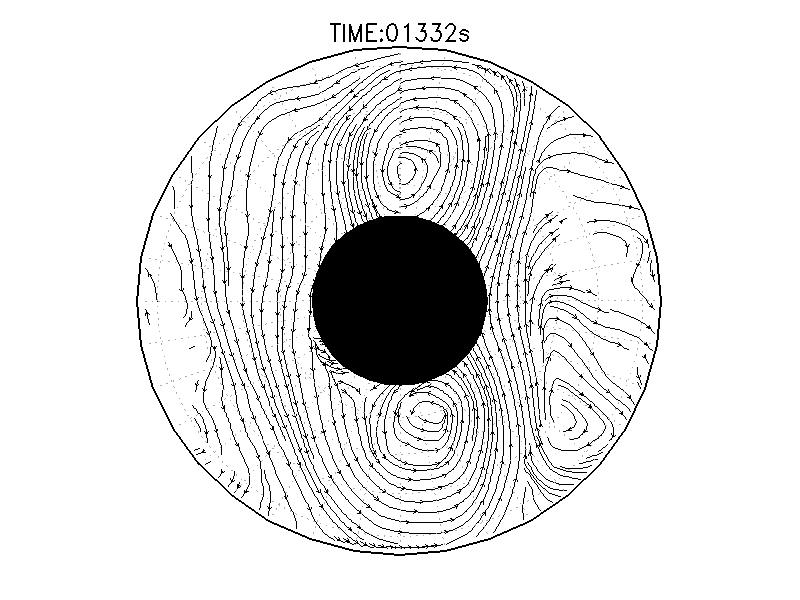
|
|||
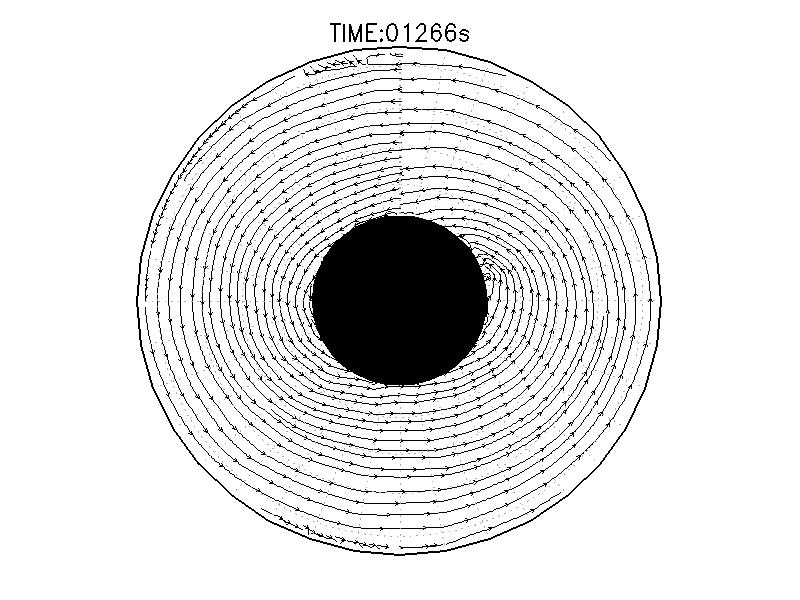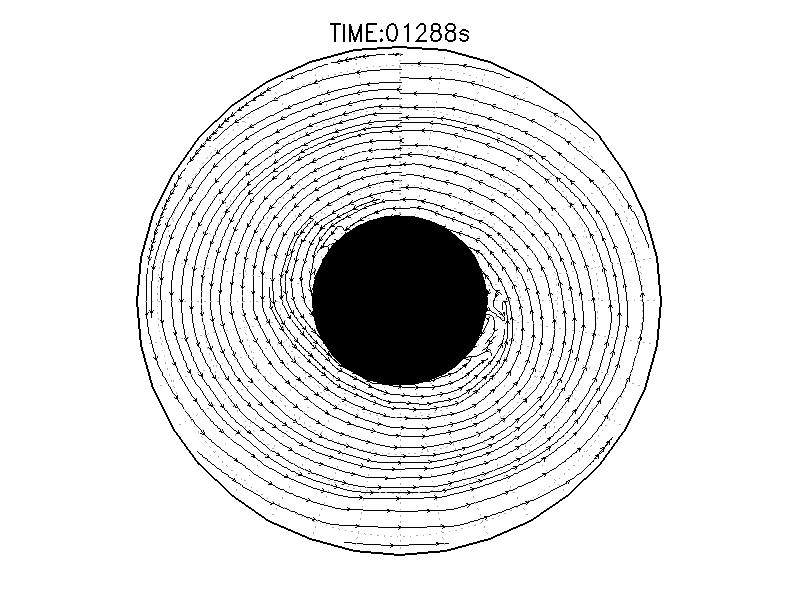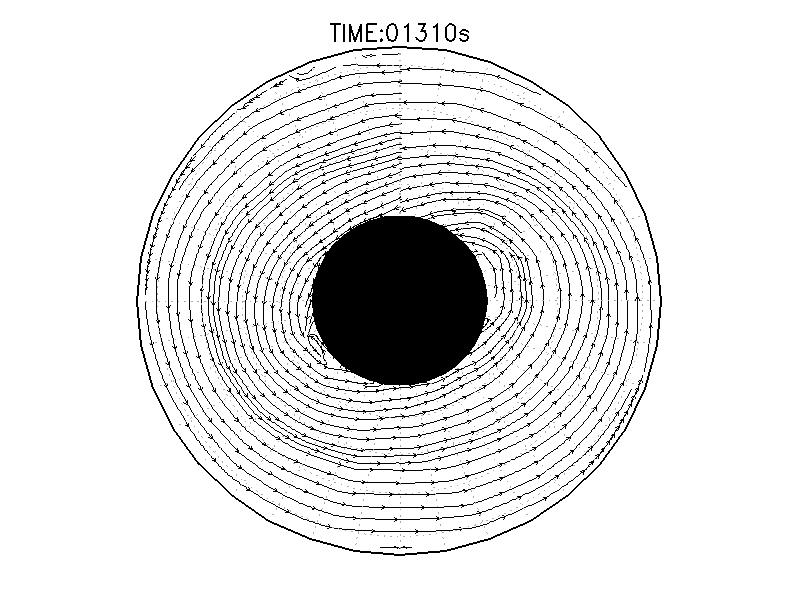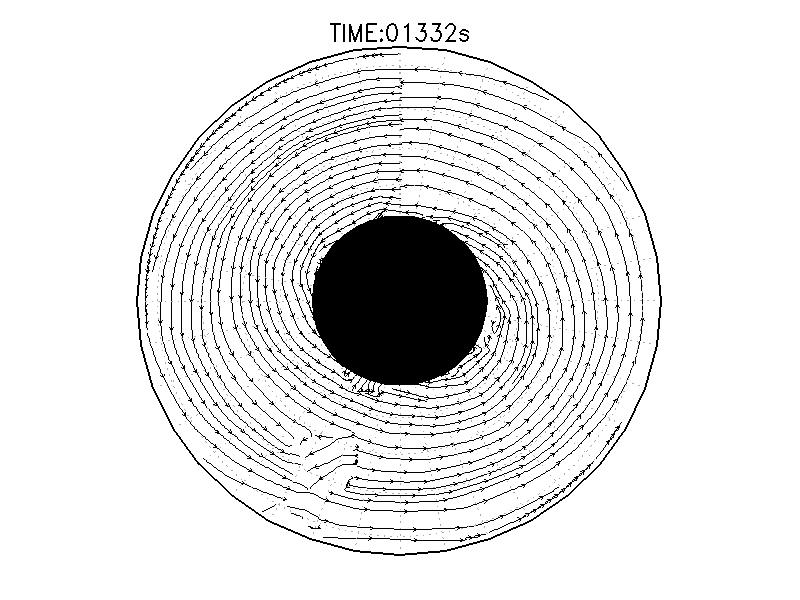
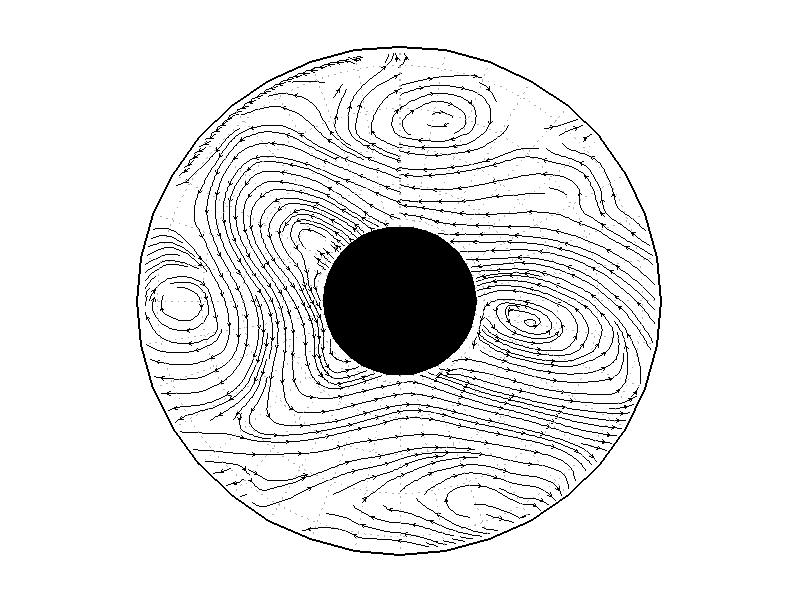
| 図3.2: 図3.1の時間と1260-1332秒の流線分布。 | |||
| (a) |
|
(b) |
|
|
|
||
| (c) |
|
||
|
|||

|
|||
| 図3.3: 図3.1の時間と1260-1332秒の速度分布。単位はmms-1。 | |||
| (a) |
|
(b) |
|
|
|
||
| (c) |
|
||
|
|||

|
|||
| 図3.4: 図3.1の時間と1260-1332秒の相対渦度分布。単位はs-1。 | |||
|
|||
| 図3.5: 実験槽中央付近(水槽幅の内側から22-44mm)で平均した実験1の相対渦度の時間変化。単位はs-1。 | |||
本研究では、PIVで検出された運動場を用いて運動エネルギーを算出する。
まず第一段階として、格子座標で得られた運動場を円筒座標系に変換し、接線方向(接線流)と半径方向(動径流)の速度成分に分解する。動径流は格子座標と同じ1.9mm間隔、接線流は1.0度間隔である。そして、運動エネルギー量(KE)は以下の式(1)で算出する。
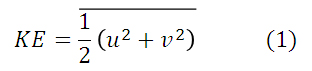
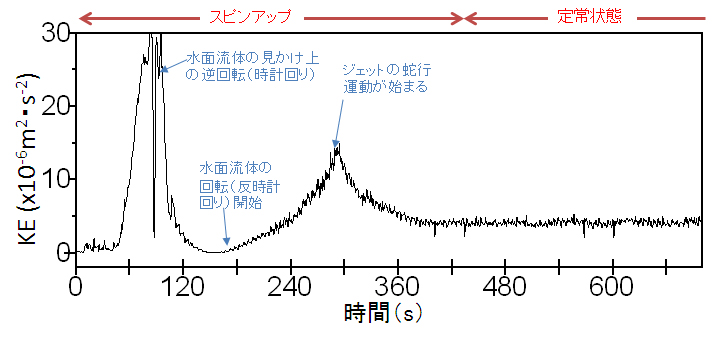
式(1)のuは接線流(反時計回りをプラス)、vは動径流(外向きをプラス)である。本研究では、KEを円周(接線)方向で平均した量を用いて議論するため、式(1)右辺に上付きバーをつける。図3.6(a)は、実験1における、実験槽中央付近(水槽幅の内側から22-44mm)で平均したKEの時間変化を表す。スピンアップ期間(約7分; 付録1)以降で定常状態となり、KEは約4.0x10-6m2s-2で変動が小さくなる。
次の第二段階は、接線流や動径流を円周方向で平均した軸対称成分と、それからの差となる非軸対称成分に分解する。例えば接線流uの運動を分解すると、
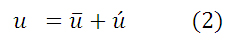
となり、式(2)右辺の上付きバーが軸対称成分、プライムが非軸対称成分である。接線流と動径流の軸対称成分と非軸対称成分に分解した場合の運動エネルギー量KEは、
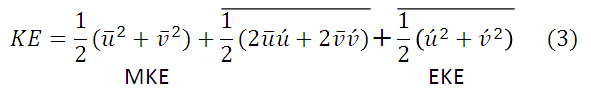
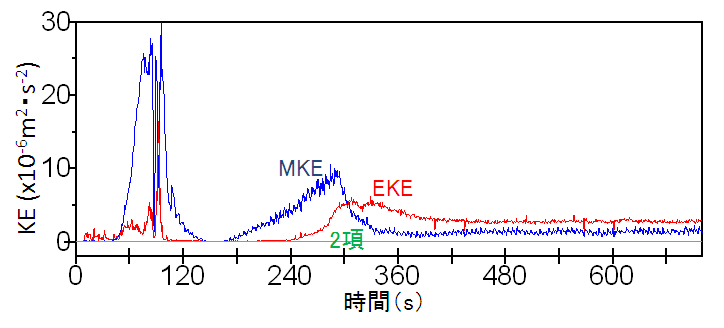
となる。第1項を平均場の運動エネルギー量(MKE)、第3項を渦運動エネルギー(EKE)と定義する。図3.6(b)のそれぞれの運動エネルギー量の時間変化を示す。式(3)右辺第2項は、他の項に比べて無視できるほど小さいため、KEはMKEとEKEのほぼ和と考えられる。MKEとEKEは、スピンアップ期間で変動が大きいものの( 付録1)、それ以降のMKEは約1.0x10-6m2s-2、EKEは約3.0x10-6m2s-2で変動が小さくなる。
第三段階として、非軸対称成分の運動をフーリエ解析により接線方向で波数分解を行った。例えば非軸対称成分の接線流を波数分解すると、
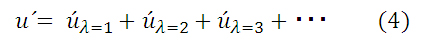
のように表される。式(4)右辺のλは波数を指す。この波数別の非軸対称成分から、渦運動量エネルギーが算出できる。例えば、波数3の非軸対称成分から求まる渦運動エネルギー量(EKE3)は、
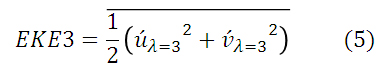
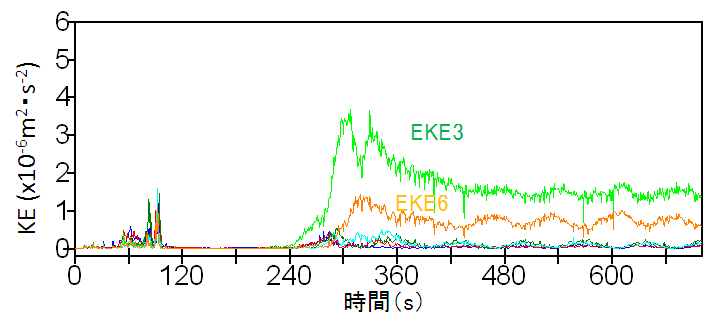
となる。波数1から9までの非軸対称成分の渦運動エネルギーの和はほぼEKEと一致したため、この波数毎の運動エネルギーの分解は妥当であることを確認した。図3.6(c)は、波数1から6までの非軸対称成分から求まる渦運動エネルギー量の時間変化である。EKE3が最も大きく、次いで波数3の高調波に当たるEKE6が大きい。それ以外の波数の渦運動エネルギー量は1桁小さい値であった。 図3.6cによると、EKE3やEKE6が、定常状態の期間でも約0.2x10-6m2s-2の大きさで約70秒の周期的な変動をしている。これは、網目上の格子データから円筒座標に変換した際に発生した、運動量の解析誤差である。一定の間隔(3つの波形が200秒で1周することを考えれば、周期70秒の変動は整合的である)で変わるジェットと格子の位置関係により見かけ上発生していて、実際にこのようなエネルギーの時間変動は起きていない。
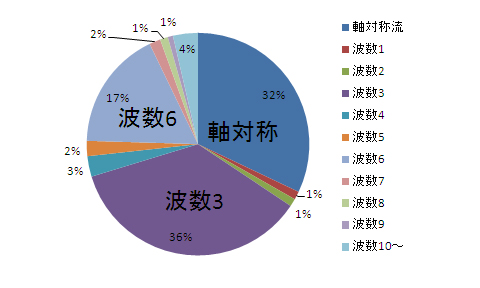
時間平均をした各運動エネルギー量を、全運動エネルギー量KEの中での割合で示したのが図3.7(a)である。EKEはKEの68%であり、MKEの32%に対して約2倍である。EKEの中でもEKE3が約半分を占めており、この傾圧不安定波は波数3が卓越波数だと同定できる。卓越波数の高調波であるEKE6もEKEの4分の一と大きい。一方、卓越波の隣の波数(サイドバンド)であるEKE2やEKE4は小さい。このサイドバンドが非常に小さいという結果は、Tamaki and Ukaji(1985)と一致している。
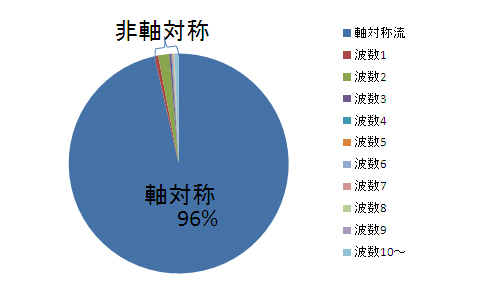
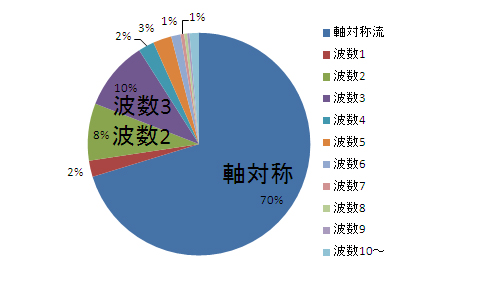
図3.7(b)と(c)は、実験2と実験3の結果である。実験2では、MKEがKEの95%と占めている。傾圧不安定波が発生していないと目視でも確認できるが、定量的にも軸対称運動が支配的であることを示している。実験3は、MKEがKEの70%に対して、EKEは30%である。EKEのなかではEKE3が最も大きいが、EKE2もそれに匹敵するほど大きい。この渦運動エネルギー量の解析でみられるように、サイドバンドの支配率が高いという結果は、実験1やTamaki and Ukaji(1985)の結果とは異なっている。
| (a) |
|
||
| (b) |
|
||
| (c) |
|
||
| 図3.6: 実験1の実験槽中央付近(水槽幅の内側から22-44mm)で平均した(a)KEの時間変化、(b)MKE(青)とEKE(赤)と式(3)右辺第2項(緑)、(c)EKEの波数1〜6のEKE。単位はx10-6m2s-2。 | |||
| (a) |
|
(b) |
|
| (c) |
|
||
| 図3.7: 時間平均したKEの中での各波数のEKEの割合。真上から右回りに、MKE(軸対称)、波数1から9EKEまで続き、波数10以上の合計のEKEの割合。(a)実験1(480〜600秒の時間平均)、(b)実験2(480〜600秒)、(c)実験3(660〜780秒)。実験3は外側円盤と内側円盤の回転速度がわずかにずれていたため、KEとMKEの算出時に補正を加えている。 | |||
| 粒子画像流速測定法と渦運動エネルギーを用いた回転水槽実験で発生する傾圧不安定波の定量化 | << Prev | Index| Next >> |