はじめに (2) 回転系における対流のレジームの遷移と水平スケール：２次元数値計算 はじめに (1) はじめに (3)

最近, Sakai6) は, スケーリング則を用いた非線形バランスを考慮し, 回転系の対流の水平スケールを導いた:

この式よって計算される水平スケールを 図1 に示す. Sakai は, 実験による対流のセル間隔が 導いた理論式と極めてよく一致することを示した. 水を作業流体とした実験を行なっており, スケーリングには対流の上昇流と下降流の温度差と 渦方向の速度との間に地衡風平衡が成立するとして水平スケールを導いた.

図1. Sakai による対流の水平スケール. 左側の斜めの直線は, レイリー数一定のときに水平スケールが極大となる位置を 結んだもの. 右側の斜めの線は, 中立曲線である. この線より下側では対流は生じない.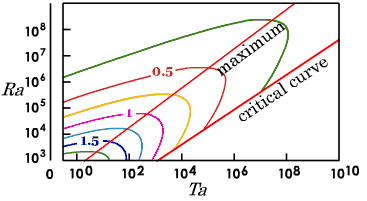

図1 に示すように, Sakai の式によって与えられる対流の水平スケールは単調な依存性をもっていない. テイラー数一定の条件のもとでは, 水平スケールはレイリー数に関して極大をもつ: レイリー数が小さい間は, レイリー数が大きくなるにつれて水平スケールは大きくなるが, さらにレイリー数が大きくなると水平スケールは逆に小さくなる. このような極大は Rossby3) の実験結果にもあらわれている. 同様に, レイリー数一定の条件のもとでは, テイラー数に対しても水平スケールの極大が存在する: テイラー数が大きくなるにつれて水平スケールが大きくなり, さらに大きくなると逆に水平スケールが小さくなる. ところが, このような水平スケールのテイラー数に対する依存性に関しては Sakai には十分な考察が加えられていない. Sakai では実験結果を容器内で生じた対流の数にのみ着目して, それから導かれた水平スケールを理論式と比較しただけであり, 理論式を導く際に用いた仮定が 本当に成立しているかどうかについての考察はなされていない.

Sakai の導いた関係は, 中立状態を十分越えた条件でのバランスを考慮したものであるため, 線形論では予想できないものである. Sakai の理論式ではテイラー数が小さいときには, 回転とともに水平スケールは大きくなる傾向にあり, 線形論の予想とは逆の依存性をもつ. このことは, Sakai が地衡風平衡を仮定して理論式を導いたことを考えれば, なんら不思議なことではない. 回転が小さいときの対流においては, 水平方向の運動方程式において 水平温度差による水平圧力勾配項とバランスするのは, 一般の非回転系でのベナール対流と同じく, 粘性項あるいは非線形項(移流項)である. このようなバランスのもとでの対流を「粘性・慣性レジーム」とよぶことにしよう. 一方, 地衡風平衡が成立する場合には, 水平方向の運動方程式において 水平温度差による水平圧力勾配項とバランスするのはコリオリ項である. このようなバランスを「地衡風レジーム」とよぶことにする. Sakai が対象にしたのは地衡風レジームの対流だけである. 一般に, 回転が大きくなるにつれて粘性・慣性レジームから 地衡風レジームへの遷移が起こることになるだろう. このような遷移が起こるのはどのようなパラメター範囲なのか, Sakai には明らかにされていない. 確かに, 補遺A に示したように, 解析的な解が求まる線型論の場合には流れの遷移が どのような条件で生じるか調べることができる. しかし, 実際の実験に対して線型論の予想が適用できる保証はない. すなわち, Sakai の理論式がどのような場合に適用可能なのかわかっていない.

はじめに (2) 回転系における対流のレジームの遷移と水平スケール：２次元数値計算 はじめに (1) はじめに (3)