| 粉体層上の動摩擦係数測定実験とその流体力学的考察 |    |
| 粉体層上の動摩擦係数測定実験とその流体力学的考察 | |
主要な結果 6から、滑走状態Bにおいては、円盤は前部が後部よりも1〜2mmほど高いことがわかる。このことから、流動化した粉体層が円盤底面に衝突し、その際、円盤に上向きの力（本論文ではこれをニュートン的揚力と呼ぶ）が発生するであろう。そこで、その大きさを見積もってみる。
|
円盤に固定された座標で考え、粉体の粒子が速度Vで円盤底面が完全弾性衝突をするとすれば、円盤が粉体から受けるニュートン的揚力 F は F = 2 r S v2 sin2q cos q となる。ここでr, S, v, q はそれぞれ、粉体の密度、円盤の底面積、円盤の速度、水平を0とした円盤の傾きである。このニュートン的揚力で底面圧力pの円盤を支えるとすれば、 v = ( p / 2 r sin2q cos q )1/2 の速度が必要となる。 |
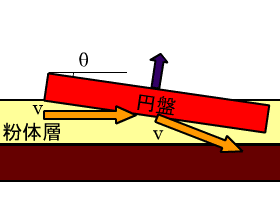 図23 ニュートン的揚力の模式図。 粉体が円盤底面で完全弾性衝突をする際に円盤が受ける力を藍色の矢印で示した。 |
ここで実験中で確認された円盤の傾き（約0.6°）、実験に用いた円盤の底面圧力745Pa、粉体の密度0.5×103kg/m3を用いてこの速度を求めると、87m/sとなる。これは実験で得られた浮上臨界速度（2〜3m/s）より遥かに大きく、このようなメカニズムで円盤が浮上していると考えるのは難しい。
|
粉体層上の動摩擦係数測定実験とその流体力学的考察 |
|