| 粉体層上の動摩擦係数測定実験とその流体力学的考察 |
円盤の底面状態が磨いた金属表面の場合よりも、粉が付着するようなざらついた底面の方がよく滑る(比較実験の結果 3)。また、円盤が通過した部分の粉は円盤の進行方向に移動している(主要な結果 5)。
以上の二点から、円盤直下で、粉体の円盤に対する相対速度が小さくなることが円盤の浮上に関係する、と考えることができる。
|
そこで、流動化した粉体を流体とみなし、相対速度の減少にともない動圧が発生し円盤を浮上させているとする(動圧モデル)。この概念を図24に示す。ただし、円盤直下以外の部分では滑走の影響が認められないこと(主要な結果 5)から、円盤直下の粉体が円盤の両脇に逃れることはないとする。 円盤直下の粉体の円盤に対する相対速度が0になるとすると、発生する動圧 p は、 p = r v2/2 で与えられる。 これから、底面圧力Pの円盤が自分自身を支えうる動圧を発生させる事ができる速度の臨界速度を求めると v = ( 2P / r )1/2 となる。 |
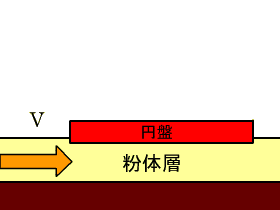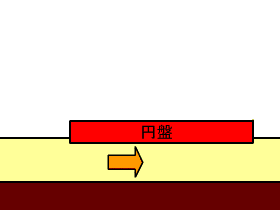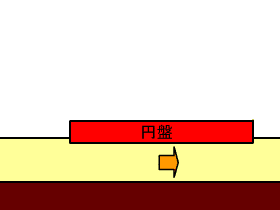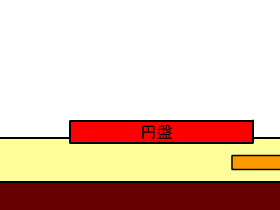 図24 動圧モデルの概念図。円盤直下で、粉体層の円盤に対する速度が小さくなると、それに応じて動圧が発生する。 |