このシナリオを確かめるために,
先の境界層理論をもとにして理論的に水平速度を見積もり,
レイリー数に対して
uh と
u,u' の大小関係を調べてみる.
鉛直対流としての水平速度は境界層理論により与えられる.
プレートの外側で形成される流れの x 方向の
速度の大きさ u は,
|
![u = \left( \Dinv{2 \sqrt{\pi}}\right)^{\frac{2}{3}}\left[ ...{a^{7}}{(1+a^{4})^{2}} \right]^{\Dinv{3}} Ra^{\frac{2}{3}},](img32.gif) |
(10) |
プレートの下での水平速度 u' を見積もるには,
(10)において
(8) の Ra' を用いればよい.
プレートがない場合および全表面をプレート覆った場合の
数値計算の結果
と比較した結果,
実際に
(10) を用いて流速を見積もる際には
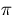 で割った値を用いることにする.
で割った値を用いることにする.
プレートによって形成される水平方向の温度差が引き起こす流れ
uh は
定常状態の運動方程式を満たしているとする.
|
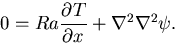 |
(11) |
(11)を z で微分して
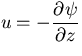 を用いると
を用いると
|
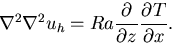 |
(12) |
温度差
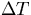 は
は
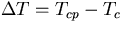 とし,
(5), (9)
を用いてレイリー数の関数としてあらわす.
対流セルの鉛直方向のスケールを Lz=1,
水平方向のスケールを Lx とすると,
とし,
(5), (9)
を用いてレイリー数の関数としてあらわす.
対流セルの鉛直方向のスケールを Lz=1,
水平方向のスケールを Lx とすると,
|
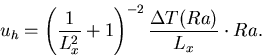 |
(13) |
この式を用いて数値的に値を求めるときには,
温度場と流線関数が
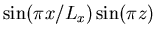 の形で表されることを考慮して
の形で表されることを考慮して
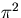 で割った値を用いる.
で割った値を用いる.
で割った値を用いることにする.
を用いると
は
とし, (5), (9) を用いてレイリー数の関数としてあらわす. 対流セルの鉛直方向のスケールを Lz=1, 水平方向のスケールを Lx とすると,
の形で表されることを考慮して
で割った値を用いる.