5.3.1 平均流の加速への寄与
帯状成分の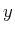 微分や
微分や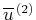 の鉛直平均がゼロであること、(4),(8)などに注意して、(17)の
の鉛直平均がゼロであること、(4),(8)などに注意して、(17)の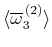 成分について書き下すと次のようになる。
成分について書き下すと次のようになる。
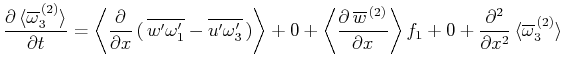 |
(26) |
第2項(基本流と二次流の相互作用の効果)と第4項(浮力の効果)はゼロとなる。第1項(擾乱同士の相互作用: 運動量輸送の効果)、第3項(二次流に働くコリオリ力の効果)、第5項(粘性の効果)、右辺の総和の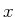 分布を図25(
分布を図25(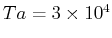 の場合は図26)に示す((25)を用いて
の場合は図26)に示す((25)を用いて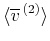 に変換)。これを見ると、第3項のコリオリ力の効果が第1項の運動量輸送の効果と逆向きに働いており、寄与が最も大きいことが分かる。第3項だけに注目し、(25)を用いると次が得られる。
に変換)。これを見ると、第3項のコリオリ力の効果が第1項の運動量輸送の効果と逆向きに働いており、寄与が最も大きいことが分かる。第3項だけに注目し、(25)を用いると次が得られる。
回転軸が鉛直な系であれば鉛直流にコリオリ力は働かないが、今は回転軸が傾いた系を扱っているため、固有モードの二次効果によって生成された鉛直流にコリオリ力が働き、平均流の加速に大きく寄与する。
図25:
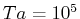 の場合の発達率最大の固有モードによる、
の場合の発達率最大の固有モードによる、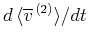 への各項の寄与。
への各項の寄与。
赤線: 第1項(擾乱同士の相互作用: 運動量輸送の効果。図23(右)に相当)、緑線: 第3項(二
次流に働くコリオリ力の効果)、青線: 第5項(粘性の効果)、紫線: 総和(図24(右)に相当)
|
|
図26:
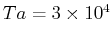 の場合の発達率最大の固有モードによる、
の場合の発達率最大の固有モードによる、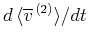 への各項の寄与。
への各項の寄与。
赤線: 第1項(擾乱同士の相互作用: 運動量輸送の効果。図23(左)に相当)、緑線: 第3項(二
次流に働くコリオリ力の効果)、青線: 第5項(粘性の効果)、紫線: 総和(図24(左)に相当)
|
|
SAITO Naoaki
2009-07-09
![]() 微分や
微分や![]() の鉛直平均がゼロであること、(4),(8)などに注意して、(17)の
の鉛直平均がゼロであること、(4),(8)などに注意して、(17)の![]() 成分について書き下すと次のようになる。
成分について書き下すと次のようになる。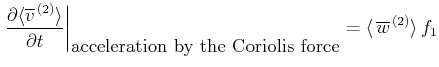
![\includegraphics[trim=0 0 5 4,clip,scale=1.28]{img2/ksA-e-FX/f316-e-FX3.ps}](img266.png)
![\includegraphics[trim=0 0 5 4,clip,scale=1.28]{img2/ksA-e-FX/f173-e1-FX3.ps}](img267.png)