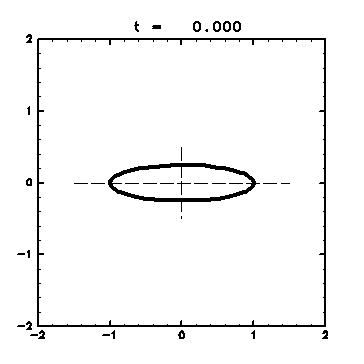
4.1 不安定な楕円渦の時間発展
4.2 楕円渦の変形に関する流線の解析
4.3 パッシブコンターによる流体混合の可視化
4.4 流体塊の変形に関する有限時間リアプノフ解析
4.5 パッシブコンター移流によるリアプノフ解析の確認

4.1 不安定な楕円渦の時間発展

初期値として楕円渦パッチに微小擾乱を加えた状態を考え、 その時間発展を計算する。楕円の扁平率や擾乱の波数に依存して、 渦パッチの時間発展の様子がどのようになるかを見る ( 堀居,1997 )。

次のような楕円を与え、その内部では渦度が一定値 q = 2π、 外部では q = 0 とする。
(4.1)
このとき楕円渦は、長軸と短軸の比λに依存して一定の角速度 γ = 2πλ/ ( 1 +λ )² で 形を変えずに回転する( Lamb,1932 )。

この楕円渦に次のような微小擾乱を加える ( Dritschel,1989 )。
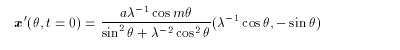(4.2)
m = 3 のとき、λ > 3 の場合には、 その楕円渦は不安定である( Love,1893 )。

ここで示し解析する実例で用いるパラメータは、以下のとおりである。 楕円の長軸と短軸の比: λ= 4 時間刻み幅: Δt = 0.1 ノード密度の定数部分: ρconst = 4.0 ノード密度の比例係数: ρ0 = 4.0 擾乱の波数: m = 3 擾乱の振幅: a = 0.005 アニメーション1: 渦パッチの時間発展(GIF animation; 351kB)。 コンターの位置を t = 0.0 から t = 14.0 まで 0.1 おきに示す。 破線は、擾乱がない場合の長軸・短軸の向きである。 ・ t = 5.0 ぐらいまでは、渦は大きな変化をせず、ほぼ一定の角速度γで回転する。 ・ その後擾乱の発達にともなって楕円渦は崩壊にむかう。 渦の一端が引き出されて、細く伸びていく。 この部分はストリーマーと呼ばれている。 ストリーマーが伸びていく状況は、冬季成層圏におけるプラネタリー波の砕波パターン ( McIntyre and Palmer,1983 )と似ている。 今の場合、コンター上にある渦度勾配によってできる波が砕波していると解釈できる。 ・ さらに時間が経過すると、ストリーマーが長く伸びて渦の周囲を取り巻く。 一方、楕円渦本体は円形に近づき、その回転角速度が増加する ( 式(2.13)参照 )。

<<index <previous next>