4.4 流体塊の変形に関する有限時間リアプノフ解析
流体塊の伸びや混合の程度を定量的に評価するために、 有限時間リアプノフ解析( Pierrehumbert,1991; Yoden and Nomura,1993 )を行う。
任意の場所における速度は、
渦度ジャンプのコンターに沿っての線積分(2.11)
によって与えられるが、 変形場 ∇u
、すなわちヤコビ行列 J も、 2.2節の手順と同様に計算できる。
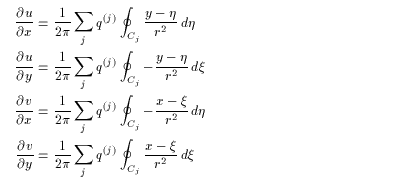 (4.7)
(4.7)
渦度ジャンプのコンターの時間発展と並行して、 レゾルベント M を求めるための線形化方程式(2.17) の時間発展も同時に行う。 初期位置は 200 x 200 の格子点状に配し、 式(4.7)にもとづいて J を計算して時間発展に使う。
いくつかの評価時間 τ に対して、各初期位置ごとに M を求めておき、 MT M の固有値より有限時間リアプノフ指数を求める。
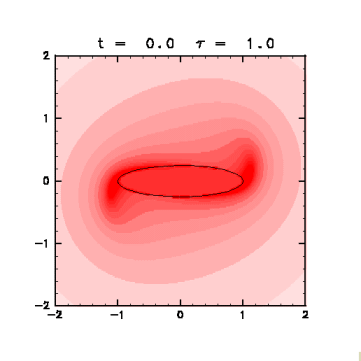
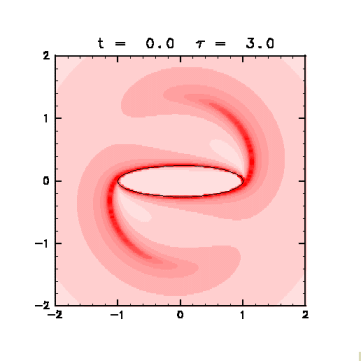
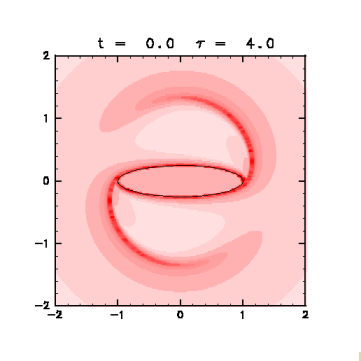
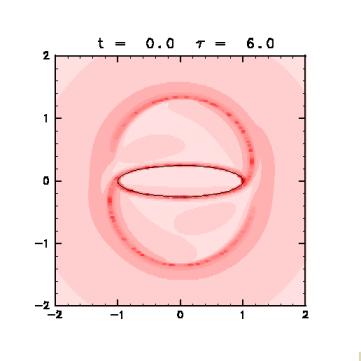
図4: 有限時間リアプノフ指数の分布(クリックすると拡大画像を表示)。
t = 0.0 を初期状態とし、 評価時間 τ
を 1.0 おきに 1.0 から 6.0
まで変えて求めた
リアプノフ指数の初期位置に対する分布を赤の濃淡で示す。
実線はコンターの位置。


![]()
・ コンター上だけでなく、 楕円渦の長軸を直径とする円の円周のすぐ外側で有限時間リアプノフ指数が大きい。 この部分の流体塊はやがてよどみ点に近づく(図5)ので、 そこで大きく引き伸ばされて指数が大きくなると考えられる。
・ τを大きくすると、リアプノフ指数の大きな部分の円弧が両端からのびていく。 評価時間内によどみ点付近に達する部分が τ とともにのびるからである。
・ 一方、渦の内部ではリアプノフ指数は小さくなっている。 渦の内部は外側と流れが分離されており、 しかもシアーによる引き伸ばしもあまりおきていないと考えられる。
・ また、渦の外側の短軸に近い領域でもリアプノフ指数は小さくなっている。 渦パッチとともに回転する系で見た流れ関数(図5)で、 時計回りの流れ(渦)がある部分に対応する。
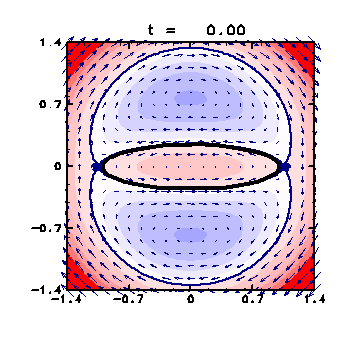 図5:
楕円渦パッチとともに回転する系からみた速度場 (クリックすると拡大画像を表示)。
図5:
楕円渦パッチとともに回転する系からみた速度場 (クリックすると拡大画像を表示)。
図2と同じで t = 0 での全体像。