4.2 楕円渦の変形に関する流線の解析
不安定な楕円渦パッチが変形していくとき、擾乱の波数 m
= 3 (奇数)の場合には
一端にストリーマーが形成され、他端には形成されない。
この違いを明らかにするために、
渦パッチとともに回転する系から見た流れ場を解析する。
流線関数 ψ( x,y,t ) は式(2.6)で与えられ、
渦度分布 Q ( x,y,t ) は式(2.2)で離散化したので、結局、次のようにかける。
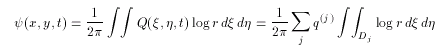 (4.3)
(4.3)
速度場と同様に、流線関数の場もコンターに沿っての線積分によって
求めることができる。
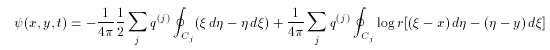 (4.4)
(4.4)
つぎに、一定角速度で回転する系から見た速度場および流線関数を考える。
系が角速度γで回転しているとき、系から見た速度場は
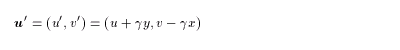 (4.5)
(4.5)
で与えられるので、回転系での流線関数は
 (4.6)
(4.6)
とかける。
角速度γが楕円渦の回転角速度であるとすると、 渦パッチの変形の初期段階にストリーマーがのびていく様子を見ることができる。
図2: 楕円とともに回転する系から見た速度場(クリックすると拡大画像を表示)。
コンターの位置を太線で示し、回転系での速度場を示す。
流線関数の等値線を細線で引き、値によって色分けをしている。
また、よどみ点を青点で示し、これらの点を含む流線を青い太線で示す。
( t = 0.0 ) 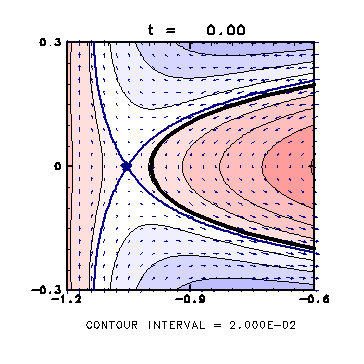

・ 初期状態では、ほとんど左右対称である。
・ よどみ点は渦パッチの外側にある。
・ よどみ点を含む流線はコンターと交わっていない。
( t = 5.0 ) 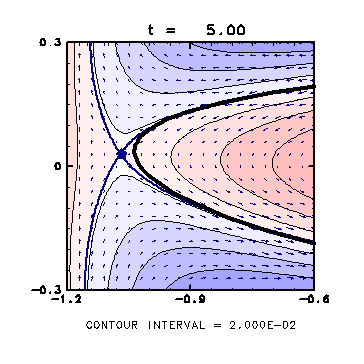
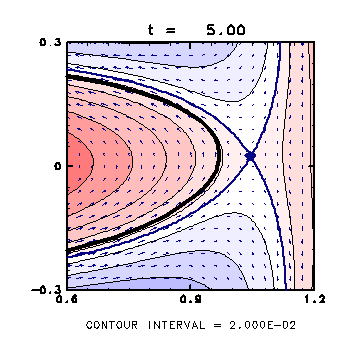
・ 左側のよどみ点が渦に近づき、
よどみ点を含む流線が渦の内側に入ってきている。
・ このあとよどみ点が渦の内側に入ってストリーマーが形成される。
・ 一方、右側のよどみ点は渦パッチから徐々に離れている。
( t = 8.0 ) 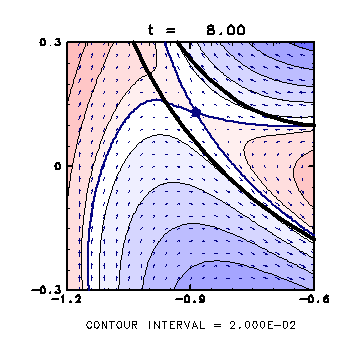

・
渦の左側では、形成されたストリーマー内部によどみ点が位置する。
・ ストリーマー付近では、コンターを横切る流れがあり、 コンターがどんどん変形されていく。
・ 一方右側では、ほぼコンターに沿った流れであり、 渦の形があまり変わらない。
一般に、よどみ点を含む流線のまわりの流体塊で、 よどみ点にむかって流れてきたものは、やがて両側に引き伸ばされていく。 Polvani and Plumb(1992) にもあるように、 渦パッチのストリーマーが伸びていくときには、よどみ点の位置が重要である。