はじめに (2) -目的

本研究では, 境界面の傾いた回転円筒内の対流に対する熱境界条件の影響を, 主に対流の水平スケールに注目して考察する. 回転円筒内の対流は, 高速に回転する球殻内の熱対流の簡単なモデルとして研究されてきている. 高速回転下ではテイラープラウドマンの定理により, 回転軸方向に伸びた一様な柱状の運動が卓越すると考えられており, このような 2 次元的な対流に上下の境界面の傾きの影響, いわゆる地形性 β 効果を考慮したモデルである. この系は回転軸が水平方向を向いていることが Dowling (1988) の扱った系と大きく異なる.

温度固定境界条件の下での回転円筒対流の性質は, Busse(1986) が線形論と弱非線形論により, Busse and Or (1986) が数値計算により調べている. さらに Brummell and Hart (1993) は高レイリー数での回転円筒対流の振舞いを数値計算により調べている. 線形安定論から予想される臨界状態の構造は回転が大きくなるにつれて対流セルの水平スケールが小さくなることが示されており, 非線形数値計算の結果からも整合的な結果が得られている. したがって, この場合にも熱境界条件と回転の影響が対流セルの大きさに関して相反する効果を与えることになる.

熱フラックス固定境界条件下での対流運動を考察しておくことは, 惑星流体核内の運動を考える際に意味のあることだと思われる. 温度固定境界条件は境界物質が無限大の熱伝導率を持つことを仮定していることになるが, 地球物理学・天体物理学的対象にて生じている対流の場合にはその意味で決して温度固定境界条件ではありえない. 実際, 流体核の熱伝導率に比較してマントルの熱伝導率が小さいので, 流体核にとっては熱伝導性の低い境界に接していることとなる. 熱フラックス固定の境界条件は熱伝導率の低い物質からなる境界に接している流体の熱対流の極限的状況に相当する.

以下では, モデルと支配方程式を示し, 線形安定論による解析を行う. さらに非線形計算による対流の時間発展の様子をみる. 最後に解釈とまとめを示す.

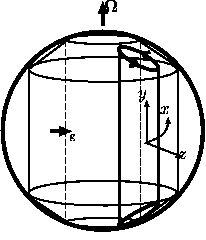図2 モデルの見取り図